Тема 3.4. Показательные и логарифмические уравнения и неравенства (10 ч).
Показательные уравнения и методы их решения.
Определение. Показательным уравнением называется уравнение, в котором неизвестное х входит только в показатели степени при некоторых постоянных основаниях.
Простейшие ПУ.
Уравнение вида 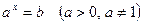 не имеет корней при
не имеет корней при 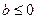 и имеет единственный корень
и имеет единственный корень 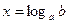 при
при 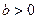 .
.
Уравнение 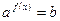 путем замены
путем замены 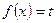 , сводится к уравнению
, сводится к уравнению 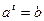 .
.
Уравнение 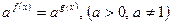 равносильно уравнению
равносильно уравнению 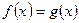 .
.
Пример 1. Решить уравнения:
а) 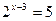 ; б)
; б) 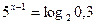 ; в)
; в) 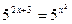 .
.
Методом последовательных упрощений.
Решение большинства ПУ после некоторых преобразований сводится к решению уравнений вида 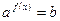 или
или 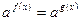 .
.
В ходе преобразований используются следующие утверждения верные при любых положительных 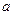 и
и 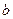 , и любых действительных
, и любых действительных 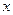 и
и 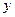 :
:
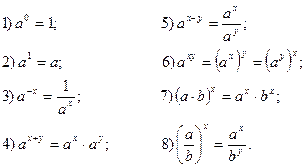
Пример 2. Решить уравнение 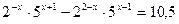 .
.
Решение. Уравнение равносильно каждому следующему:
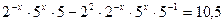
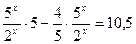
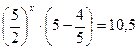
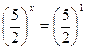
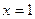
Ответ. 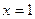 .
.
 2015-05-13
2015-05-13 387
387







