Решение простейших показательных неравенств.
Любое показательное неравенство после некоторых преобразований приводится к неравенству вида 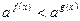
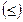 . Неравенство, в свою очередь, заменяется неравенством, связывающим показатели
. Неравенство, в свою очередь, заменяется неравенством, связывающим показатели 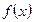 и
и 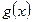 . При этом переходе нужно учитывать, что функция
. При этом переходе нужно учитывать, что функция 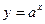 убывает, если
убывает, если 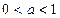 и возрастает, если
и возрастает, если 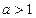 .
.
Если 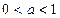 , то неравенство
, то неравенство 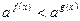 равносильно неравенству
равносильно неравенству 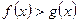 .
.
Если 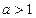 , то неравенство
, то неравенство 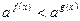 равносильно неравенству
равносильно неравенству 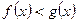 .
.
Неравенство 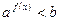 можно свести к неравенству
можно свести к неравенству 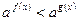 , если представить
, если представить 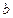 как
как 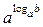 .
.
Пример 1. Решить неравенство:
а) 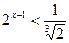 ; б)
; б) 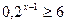 ; в)
; в) 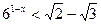 ; г)
; г) 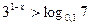 .
.
 2015-05-13
2015-05-13 436
436








