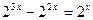
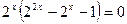
Т.к. 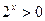 при всех х, то предыдущее уравнение равносильно следующему
при всех х, то предыдущее уравнение равносильно следующему
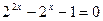
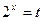 ,
, 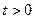
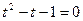
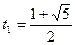 ,
, 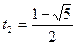
Условию 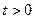 удовлетворяет только
удовлетворяет только 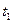 . Значит
. Значит
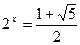
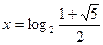
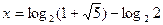
Ответ: 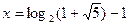 .
.
Методом замены решаются однородные показательные уравнения, т.е. уравнения вида 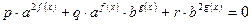 . Общий прием решения таких уравнений состоит в делении обеих его частей на выражение
. Общий прием решения таких уравнений состоит в делении обеих его частей на выражение 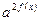 (или
(или 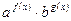 , или
, или 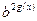 ) и последующей замене переменной. Эта операция не приводит ни к потере, ни к приобретению корней, поскольку выражения- делители при любых значениях переменной принимают только положительные значения.
) и последующей замене переменной. Эта операция не приводит ни к потере, ни к приобретению корней, поскольку выражения- делители при любых значениях переменной принимают только положительные значения.
Пример 5. 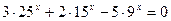 .
.
Решение. Перепишем уравнение в виде 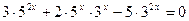 и поделим обе его части на
и поделим обе его части на 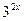 (т.к
(т.к 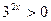 , то это не ведет к потере корней). Уравнение примет вид
, то это не ведет к потере корней). Уравнение примет вид 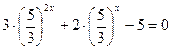 . Делаем замену
. Делаем замену 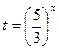 ,
, 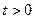 , получим уравнение
, получим уравнение 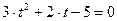 , корнями которого являются
, корнями которого являются 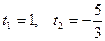 . Условию
. Условию 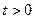 удовлетворяет только первый корень. Значит
удовлетворяет только первый корень. Значит 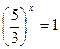 ,
, 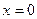 .
.
Ответ: 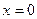 .
.
 2015-05-13
2015-05-13 514
514








