Пусть функция задана параметрически: 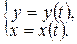 где
где 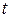 – вспомогательная переменная, называемая параметром.
– вспомогательная переменная, называемая параметром.
Нужно найти 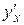 . Предположим, что
. Предположим, что 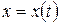 имеет однозначную обратную функцию
имеет однозначную обратную функцию 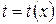 . Продифференцируем уравнение
. Продифференцируем уравнение 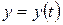 по
по 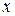 , как сложную функцию, считая
, как сложную функцию, считая  промежуточным аргументом, зависящим от
промежуточным аргументом, зависящим от 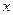 :
: 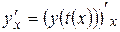 ;
; 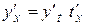 . Так как
. Так как 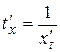 , то получим:
, то получим:
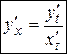 . (4)
. (4)
Пример Пусть 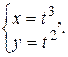 Найти
Найти 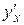 .
.
Решение. По формуле (4), получаем 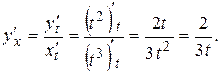
Производную функции одной переменной в некоторых случаях можно найти значительно проще, если функцию предварительно прологарифмировать, такой метод называется логарифмическое дифференцирование.
Логарифмическое дифференцирование обычно применяется при отыскании производной от степенно-показательной функции и от произведения функций, т.е. в тех случаях, когда обычными методами производную нельзя найти, либо вычисление производной очень громоздко. Конечно, эта операция может применяться и в других случаях.
Определение. Функция 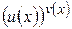 , у которых основание и показатель степени есть функции независимых переменных, называются степенно-показательными.
, у которых основание и показатель степени есть функции независимых переменных, называются степенно-показательными.
Производные таких функций вычисляются только с помощью логарифмического дифференцирования.
Пример Дана функция 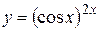 . Найти
. Найти 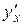 .
.
Решение. Прологарифмировав функцию 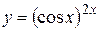 , получим
, получим
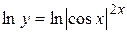
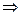
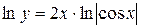 .
.
Дифференцируем полученное уравнение по 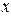 :
: 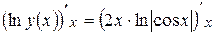
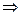
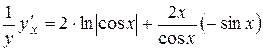 . Из последнего равенства найдем
. Из последнего равенства найдем 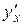 :
:
 .
.
 2015-05-13
2015-05-13 1020
1020








