Рассмотрим функцию 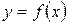 , имеющую в точке
, имеющую в точке 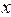 отличную от нуля производную:
отличную от нуля производную: 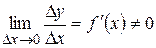 . По теореме о связи функции, ее предела и бесконечно малой функции, можно записать
. По теореме о связи функции, ее предела и бесконечно малой функции, можно записать 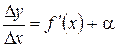 , где
, где 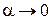 при
при 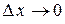 , или
, или 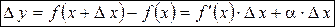 . Приращение функции
. Приращение функции 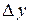 представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых 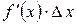 и
и 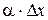 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 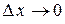 . Заметим, что
. Заметим, что 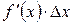 - бесконечно малая функция одного порядка с
- бесконечно малая функция одного порядка с 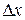 , так как
, так как 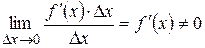 , а
, а 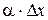 - функция более высокого порядка, чем
- функция более высокого порядка, чем 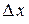 :
: 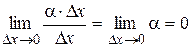 .
.
Определение. Слагаемое 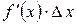 называется главной частью приращения функции
называется главной частью приращения функции 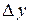 .
.
Определение. Дифференциалом функции 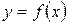 в точке
в точке 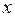 называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 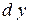 или
или 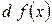 . Заметим, что
. Заметим, что
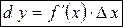 . (5)
. (5)
Определение. Дифференциал 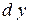 называется дифференциалом первого порядка.
называется дифференциалом первого порядка.
Дифференциал независимой переменной равен приращению этой переменной:
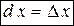 . (6)
. (6)
В самом деле, так как 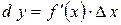 и
и 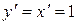 , то
, то 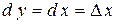 .
.
Определение. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной:
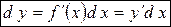 . (7)
. (7)
Так как 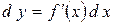 , то
, то 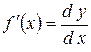 – отношение дифференциалов
– отношение дифференциалов 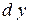 и
и 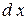 .
.
Пример Найти дифференциал функции 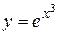 .
.
Решение. По формуле 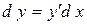 находим:
находим:
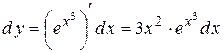 .
.
Пример Найти полное приращение функции 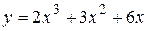 и ее дифференциал, сравнить их значения при
и ее дифференциал, сравнить их значения при 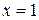 .
.
Решение. Полное приращение запишем в виде:
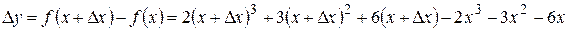 . Преобразуем это выражение:
. Преобразуем это выражение: 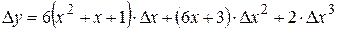 . По определению найдем полный дифференциал:
. По определению найдем полный дифференциал: 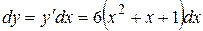 . Подставив
. Подставив 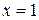 , получим,
, получим, 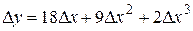 и
и 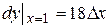 .
.
Приращение любой дифференцируемой функции приближенно с большой точностью можно вычислить при помощи равенства: 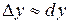 .
.
Приращение 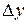 функции
функции 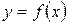 в точке
в точке 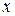 можно представить в виде
можно представить в виде 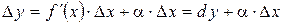 , где
, где 
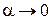 при
при 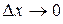 . Отбросим бесконечно малую
. Отбросим бесконечно малую 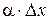 более высокого порядка, чем
более высокого порядка, чем 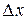 , получим приближенное равенство:
, получим приближенное равенство: 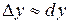 . Чем меньше
. Чем меньше 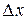 , тем точнее равенство.
, тем точнее равенство.
Так как 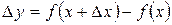 ,
, 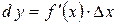 , то из равенства
, то из равенства 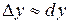 или
или 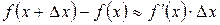 получим формулу для вычислений приближенных значений функци:
получим формулу для вычислений приближенных значений функци:
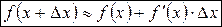 (8)
(8)
Пример Вычислить приближенно приращение функции 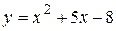 при изменении
при изменении 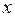 от значения 2 к значению 2,02.
от значения 2 к значению 2,02.
Решение. Так как достаточно малых 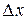 :
: 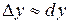 (
(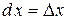 ).
).
Найдем 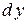 :
: 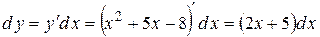 . Вычислим
. Вычислим 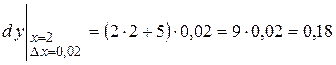 . Итак,
. Итак, 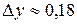 .
.
Определение. Производная, взятая от первой, называется производной второго порядка; производная, взятая от производной второго порядка, называется производной третьего порядка и т.д.:
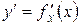 ;
;
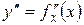 ;
;
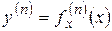 .
.
Определение. Производной 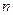 -го порядка называется производная, взятая от производной
-го порядка называется производная, взятая от производной 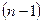 -порядка.
-порядка.
Пример Найти производную 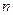 -го порядка от функции
-го порядка от функции 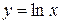 .
.
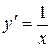 ;
; 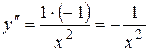 ;
; 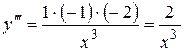 ;
;
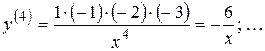
 2015-05-13
2015-05-13 1797
1797