Синтез и анализ гибридных моделей стохастических зависимостей в условиях наличия их частного описания

Традиционные гибридные модели (см. пункт 3.6) сочетают в одном решающем правиле преимущество параметрических и непараметрических аппроксимаций. При этом единое решающее правило образуют параметрическая модель восстанавливаемой зависимости и непараметрическая оценка функции невязки, которые строятся в одном и том же пространстве переменных.

Особенность рассматриваемых модификаций гибридных моделей состоит в том, что искомая зависимость 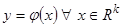представлена обучающей выборкой 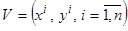и имеется её частное описание 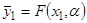в ограниченном пространстве контролируемых признаков 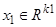, 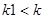. Для максимального учёта априорных сведений предлагается на основе принципов гибридного моделирования объединить в одном решающем правиле частное описание 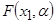и информацию об искомой зависимости, содержащейся в обучающей выборке .

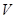Актуальность рассматриваемой проблемы подтверждается перспективностью применения методики её решения при исследовании статических объектов в условиях наличия их частных описаний 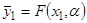, где 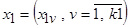, 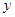- соответственно входные и выходные переменные. При появлении возможности контроля дополнительного набора компонент входных переменных изучаемого объекта 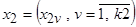, оказывающих существенное влияние на изменение выходной переменной 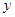, возникает необходимость построение модели зависимости 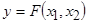на основании априорной информации 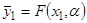и экспериментальных данных .

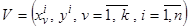Пусть об искомой однозначной зависимости 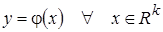известно её частное описание относительно некоторого ограниченного набора признаков

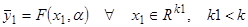
и выборка 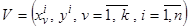экспериментальных данных, составленная из статистически независимых значений переменной 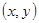исследуемой зависимости .

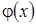Задача состоит в построении модифицированной гибридной модели 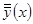искомой зависимости, совмещающей в одном решающем правиле всю имеющуюся априорную информацию.

Синтез модифицированной гибридной модели с учётом частного описания. На первом этапе синтеза структуры модифицированной гибридной модели, используя статистическую выборку 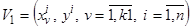, проводится идентификация параметров 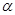модели .

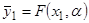Далее формируется выборка

,

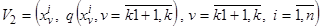составленная из значений функции невязок (3.39), например

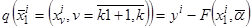
между экспериментальными данными и параметрической моделью 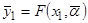в пространств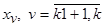е , где 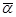- оценки параметров 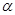модели .

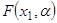Для восстановления функции невязок по выборке 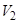воспользуемся непараметрической регрессией (3.5)

,

,

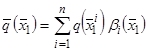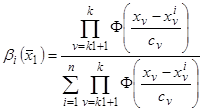где 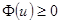- ядерная функция, удовлетворяющая свойствам

, , .

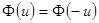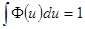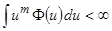Тогда гибридная модель стохастической зависимости с учётом её частного описания 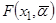представляется статистикой

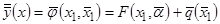. (3.40)

Асимптотические свойства гибридной модели (3.40) определяются следующим утверждением.

Теорема 3.4. Пусть: 1) восстанавливаемая зависимость 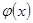представима суммой однозначных функций 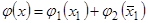; 2) функции 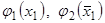и плотности вероятности 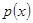, , 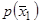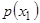ограничены вместе со своими производными до второго порядка включительно; 3) 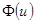- относится к классу ограниченных, положительных, симметричных и нормированных функций; 4) последовательность параметров 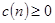ядерных функций 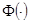такова, что при 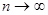значения 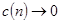, а 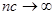. Тогда модифицированная гибридная модель (3) обладает свойствами асимптотической несмещённости и состоятельности.