2015-05-13
395
Пусть при восстановлении однозначной многомерной стохастической зависимости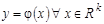 
имеется обучающая выборка 
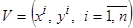малого объёма. Наиболее эффективным направлением восстановления исходной зависимости 
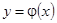в условиях малой выборки большой размерности является использование последовательных процедур принятия решений, что достигается путём разбиения исходной задачи на ряд взаимосвязанных более простых задач. Такая схема используется, например, в методе динамического программирования и методе группового учёта аргументов (МГУА).
С позиции последовательных процедур принятия решений рассмотрим модификацию МГУА с учётом на каждом этапе многоуровневого алгоритма оценок функций невязок частных непараметрических моделей.
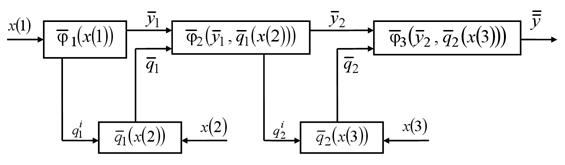
Рис. 3.12. Структура непараметрического гибридного решающего правила, основанного на учёте функций невязок
Этапы формирования алгоритма:
1. Построить модель искомой зависимости относительно первого набора признаков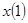 
, например с использованием непараметрической регрессии (3.5)
,
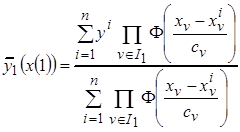где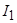 
- множество номеров признаков первой группы 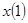. Определить оптимальный набор коэффициентов размытости 
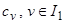из условия минимума среднеквадратической ошибки аппроксимации.
2. Сформировать выборку невязок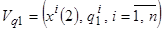 
, где значения 
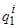можно формировать в соответствии с процедурами (3.39), например, воспользуемся выражением типа разность
.
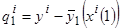3. Восстановить функцию невязок по выборке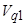 
в пространстве набора признаков второй группы 
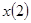с помощью непараметрической регрессии
,
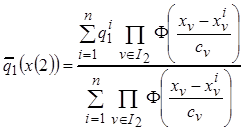где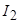 
- множество номеров признаков второй группы 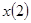. Из условия минимума среднеквадратической ошибки аппроксимации найти оптимальный набор коэффициентов 
.
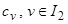4. Построить модель искомой зависимости по выборке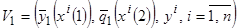 
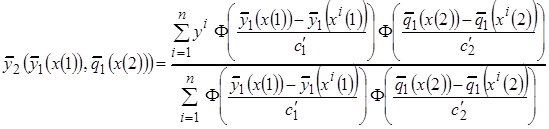
и определить оценки оптимальных коэффициентов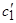 
и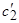 
.
5. По аналогии с пунктом 2 сформировать выборку невязок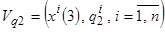 
, где значения 
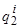можно формировать в соответствии с процедурами (3.39)
.
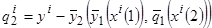6. Оценить функцию невязок по выборке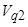 
в пространстве набора признаков второй группы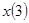 
,
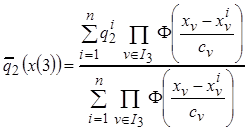где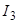 
- множество номеров признаков третьей группы 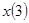. Из условия минимума среднеквадратической ошибки аппроксимации найти оптимальный набор коэффициентов 
.
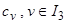7. По выборке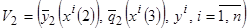 
построить обобщённую модель искомой зависимости
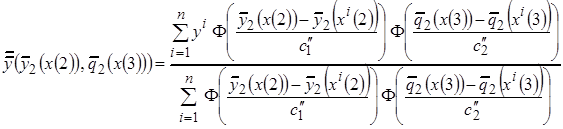
и определить оценки оптимальных коэффициентов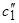 
и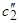 
.
Разнообразие функций невязок (3.39) порождает множество модификаций последовательных процедур формирования решений, например рис. 3.13.
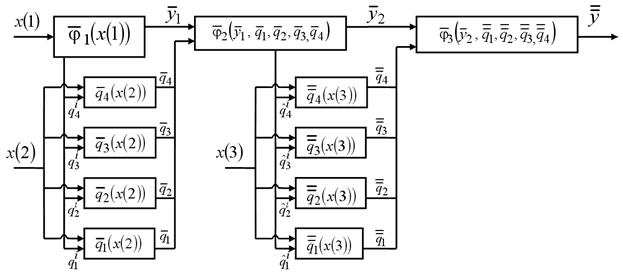
Рис. 3.13. Модификация непараметрического гибридного решающего правила, основанного на учёте разнотипных функций невязок (3.39)
