2015-05-13
410
Пусть при восстановлении однозначной зависимости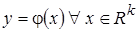 
(3.19) кроме выборки 
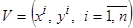, известны частичные сведения (либо принимается гипотеза) 
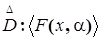(рис. 3.2) о виде преобразования 
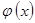с точностью до набора параметров 
.
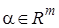Увеличение объема априорной информации и требование наиболее полного ее использования в задаче восстановления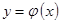 
позволяют расширить область применения принципов теории обучающихся систем. Один из эффективных подходов решения указанной проблемы состоит в предварительном исследовании аппроксимационных свойств 
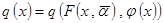параметрической модели 
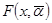зависимости 
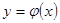путем организации вычислительного эксперимента на статистических данных V с формированием «рабочей» выборки 
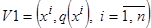. По полученной информации 
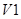восстанавливается зависимость 
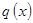, представляющая собой функцию невязки между 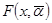и 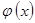с помощью непараметрической процедуры. Гибридная модель формируется как некоторая комбинация 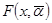и 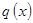, зависящая от введённого преобразования 
.
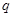Выберем одно из предлагаемых преобразований:
, 
,
, 
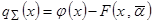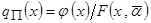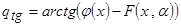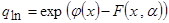, (3.37)
тогда гибридная модель запишется соответственно в виде:
, 
,
, 
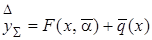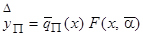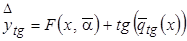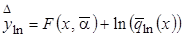. (3.38)
Построение параметрической модели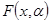 
зависимости 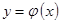по выборке 
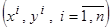и оценивание её параметров может быть осуществлено на основании хорошо разработанного аппарата многомерного регрессионного анализа (см. пункт 3.2).
Преобразование 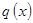восстанавливается с помощью непараметрической регрессии (см. пункт 3.3):
, 
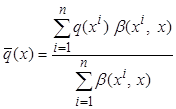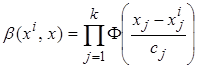
по значениям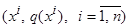 
.
При синтезе алгоритмов (3.38) формирование значений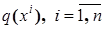 
на основании выборки 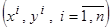осуществляется по формулам
, 
,
, 
, 
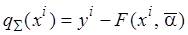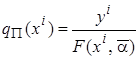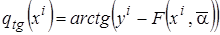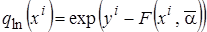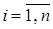. (3.39)
Ядерные функции F(×) в непараметрической регрессии соответствуют компонентам вектора x =(x 1, …, x 2) и удовлетворяют условиям положительности, нормированности и симметричности.
Кроме отмеченных выше преимуществ гибридных алгоритмов типа (3.38) следует отметить снижение требований к точности оценивания параметров a по сравнению с параметрическими моделями.
На рис. 3.10 наглядно показана информация о виде зависимости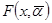 
, представляющая собой кривую и выборка объёмом 10 точек, а также значения функции невязки .
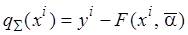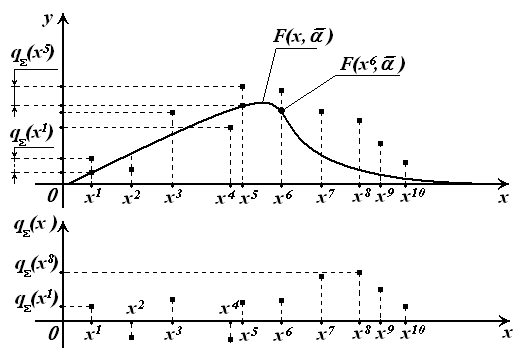
Рис. 3.10 Графическая иллюстрация формирования выборки невязок для гибридной модели .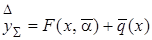
Исследование асимптотических свойств гибридных моделей. Рассмотрим задачу оценивания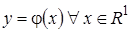 
по выборке независимых и идентично распределенных случайных величин 
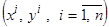при известной плотности вероятности p (x).
Предположим, что p (x) ограничена и непрерывна со всеми своими производными до порядка m включительно, причем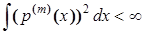 
. Эти условия, накладываемые на p (x), обозначим через Gm.
Тогда справедлива
Теорема 3.3. Пусть: 1) j(x), F(x, a) и p(x)¹0 в области определения y=j(x) удовлетворяют условиям G2; 2) функция F(u)ÎH и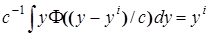 
; 3) последовательность коэффициентов размытости ядерных функций c=c(n)®0 при n®¥, а nc®¥. Тогда гибридные модели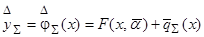 
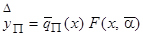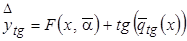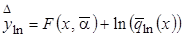, , обладает свойствами асимптотической несмещенности и состоятельности.
