| i | xi | yi | zi | zi 2 | ziyi |
| 0,10000 | 0,010000 | 3,20000 | |||
| 0,08333 | 0,006944 | 2,33333 | |||
| 0,06667 | 0,004444 | 1,46667 | |||
| 0,05660 | 0,002500 | 1,00000 | |||
| 0,04000 | 0,001600 | 0,64000 | |||
| 0,03704 | 0,001372 | 0,55556 | |||
| 0,03333 | 0,001111 | 0,33333 | |||
| Σ | 0,41037 | 0,027972 | 9,52890 |
Отсюда 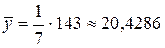 ,
, 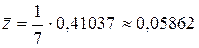 . Для вычисления оценок параметров воспользуемся формулами (1.5):
. Для вычисления оценок параметров воспользуемся формулами (1.5):
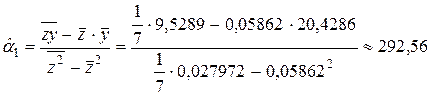 ;
;
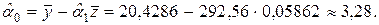
Если же оценивать параметры с помощью функции ЛИНЕЙН (Microsoft Excel), т.е. практически с неограниченной степенью точности, то получим следующие результаты: 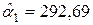 и
и 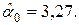
Таким образом, искомое регрессионное уравнение имеет вид: 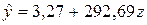 или
или 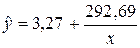 .
.
Полиномиальная модель (1.15) может быть преобразована к линейной модели введением переменных z 1= x, z 2= x 2, …, zk = xk. В результате получается так называемая линейная модель множественной регрессии (переменная y зависит от нескольких переменных zj). В следующей главе будут рассмотрены вопросы определения параметров такого уравнения и показателей его качества.
Второй класс. Модели, нелинейные по параметрам, но сводящиеся к модели, линейной по параметрам, с помощью некоторого математического преобразования.
Примерами таких моделей могут служить показательная (экспоненциальная) и степенная регрессионные модели, в которые случайная компонента ε входит в качестве сомножителя (или, как говорят, мультипликативным образом):
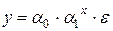 , (1.17)
, (1.17)
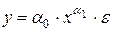 (1.18)
(1.18)
Обе модели сводятся к модели, линейной по параметрам, путем логарифмирования. Покажем это на примере показательной модели (1.17). Имеем:
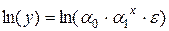 .
.
Используя свойства логарифма, выполним преобразования:
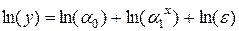
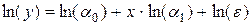
Полученная модель уже является линейной по параметрам. Вводя новые переменные и обозначения: u =ln(у), ε *=ln(ε), a 1*=ln(a 1), a 0*=ln(a 0), получим
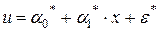 (1.19)
(1.19)
Рассчитав значения переменной u по заданным наблюдениям yi переменной у, можно оценить параметры уравнения (1.19) с помощью известных методов. По найденным оценкам легко определить и параметры исходного нелинейного уравнения (1.17).
Важно отметить, что применение МНК для оценки параметров уравнения (1.19) предполагает выполнение требований классической линейной модели (см. параграф 1.2). Проверка статистической значимости параметров и регрессии в целом на основе t- и F -статистик имеет смысл только в том случае, если компонента 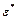 , т.е ln(ε), распределена нормально.
, т.е ln(ε), распределена нормально.
Третий класс. Собственно нелинейные модели, т.е. модели, которые нельзя свести к модели, линейной по параметрам.
Например, это – та же показательная модель, но в которую случайная компонента ε входит аддитивным образом, т.е. в качестве слагаемого:
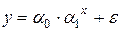 (1.20)
(1.20)
Для оценивания параметров таких моделей используется так называемый нелинейный метод наименьших квадратов, основанный на непосредственном решении задачи оптимизации
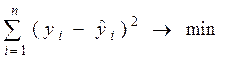
теми или иными численными методами.
В данном учебном пособии этот метод не рассматривается.
 2015-05-13
2015-05-13 547
547








