Резонанс токов

Резонанс токов наблюдается в параллельных ветвях. При резонансе токов по фазе совпадают ток общей ветви и напряжение на параллельном участке. Рассмотрим резонанс токов в схеме с параллельными ветвями RL и RC (рис. 4.11, а).

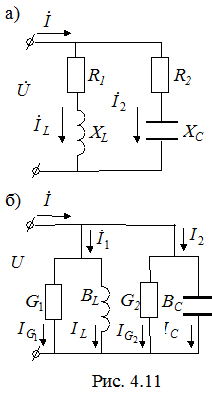Заменим данную схему эквивалентной, приведенной на рис. 4.11, б.

В этой схеме приняты следующие обозначения:

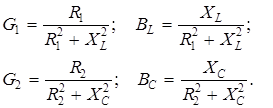(4.8)

Для данной схемы справедливо

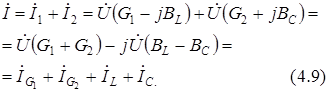
В режиме резонанса 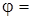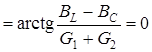. Это возможно, если будет выполнено условие

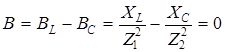(4.10)

и соответственно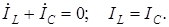

При резонансе полная мощность, которая потребляется контуром, минимальна и носит активный характер

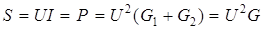. (4.11)

В режиме резонанса ток на входе параллельного контура 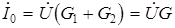, т.е. минимальный ток для этой схемы при неизменном напряжении на входе 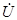. При G ® 0 I ® 0. Сопротивление такой цепи Z ® ¥. Для резонансной частоты w₀такой контур принято называть фильтром - пробкой.

Величина резонансной частоты для приведенной схемы определяется из условия

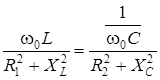. (4.12)

Приведя к общему знаменателю и умножив обе части на w₀, после преобразований получим

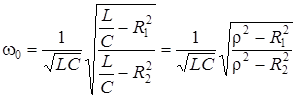. (4.13)

Резонанс в такой схеме может иметь место, если только выполняются следующие условия:

1) ;

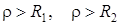2) .

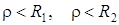При 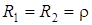схема находится в резонансе при любых частотах. Это так называемый всеволновой резонанс.

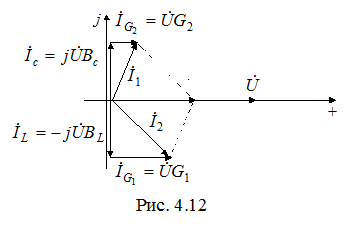Основой для построения векторной диаграммы является описание схемы с помощью выражения (4.9). При построении совместим с вещественной осью напряжение

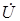, тогда векторная диаграмма будет иметь вид, представленный на рис. 4.12, если учесть, что

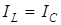Под добротностью контура при резонансе токов понимают отношение тока на реактивных элементах I_L или I_С к току на входе контура I

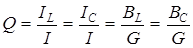. (4.14)

При незначительных потерях в контуре токи I_L и I_C могут многократно превышать токи на входе схемы.

4.2.1. Частотные и резонансные характеристики в параллельном LC - контуре

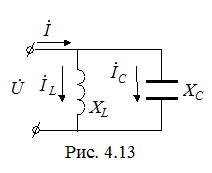В качестве частотных характеристик в контуре на рис. 4.13 выступают зависимости 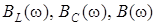, значения которых при приведены в табл. 4.3.

Характер изменения зависимостей 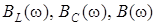приведен на рис. 4.14.

Таблица 4.3

w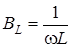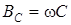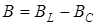
	¥		¥
w₀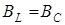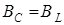
¥		¥	¥

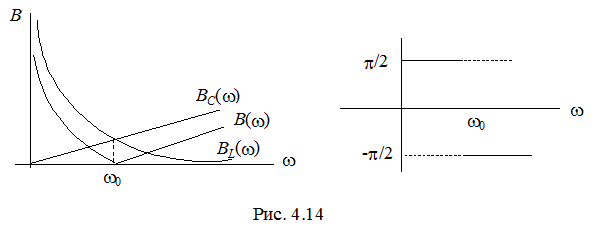Учитывая, что , характер резонансных кривых 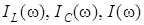полностью совпадает с соответствующими частотными зависимостями. При такой контур выполняет роль фильтра – пробки, проводимость его, а следовательно, и ток 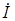общей ветви, равны нулю, а сопротивление – бесконечности.