2015-05-13
1442
Пусть в последовательной цепи, состоящей из R, L, C элементов, протекает ток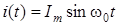 
, тогда напряжение на емкости 
.
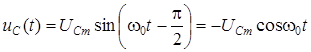Магнитная энергия индуктивности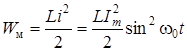 
. Энергия, накопленная на емкости 
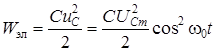. Поскольку 
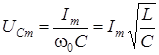, то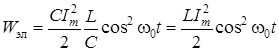 
. В каждый момент времени суммарная энергия контура в режиме резонанса
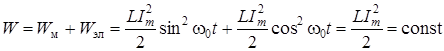, (4.6)
т.е. в контуре происходит обмен энергии между индуктивностью и емкостью. Сумма энергий магнитного и электрического полей остается неизменной. Энергия, которая потребляется от источника, равна только тепловой, выделяемой на активном сопротивлении контура.
4.1.2. Частотные и резонансные характеристики последовательного RLC -контура
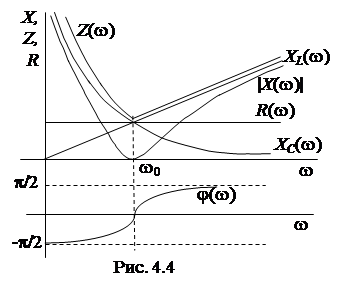Зависимости параметров контуров RLC -контура от частоты называют частотными характеристиками. Это индуктивное сопротивление 
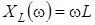, емкостное сопротивление 
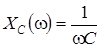, реактивное сопротивление 
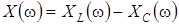, активное сопротивление 
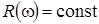, полное сопротивление
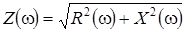, угол сдвига фаз 
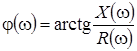. Качественный вид этих характеристик приведен на рис. 4.4.
В момент резонанса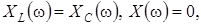 
.
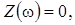
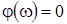Зависимости тока I (w), напряжения на индуктивности UL (w),напряжения на емкости UC (w) называют резонансными характеристиками.
|
|
|
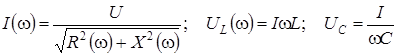. (4.7)
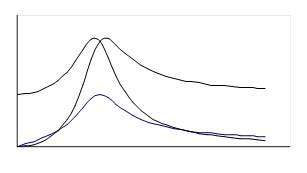| Графики этих характеристик при добротности Q = 2 представлены на рис. 4.5. При добротности контура Q < 5 максимумы напряжений UL и UC смещаются друг от друга на одно и то же значение частоты от резонансной w0. При добротности контура Q > 5 максимумы этих напряжений при резонансной частоте w = w0сливаются. |
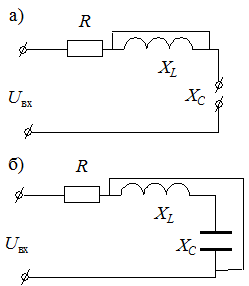Если частота w = 0, то XC = ¥, XL =0 (рис. 4.6, а). При этом условии
.
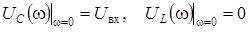Если частота равна резонансной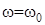 
, то X = 0 (рис. 4.6, б). При этом 
.
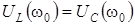Если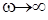 
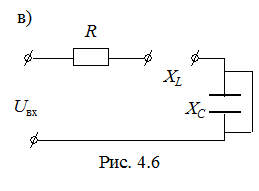
, тогда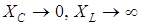 
(рис. 4.6, в). При этом 
.
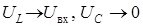Из приведенных характеристик следует, что RLC - контур обладает избирательными свойствами. Самое большое значение тока имеет место в режиме резонанса (w = w0). Для оценки избирательных свойств контура вводят понятие полосы пропускания контура. Она равна разности частот, которым соответствует отношение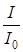 
до и после резонанса, равное 
.
 
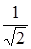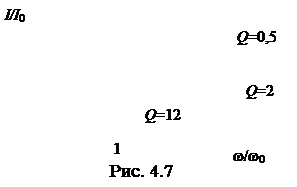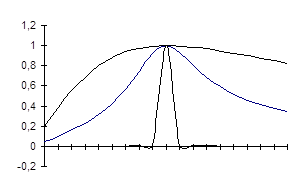| Параметры цепи оказывают большое влияние на избирательность. Чем больше добротность контура, тем выше его избирательность. В этом можно убедиться при рассмотрении кривых на рис. 4.7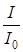
( – отношение тока текущей
|
частоты к току резонансной частоты;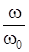 
– отношение текущей частоты к резонансной. Чем больше добротность контура, тем лучше его избирательные свойства и тем меньше полоса пропускания.
4.1.3. Зависимости I, UL, UC от L и С
 |
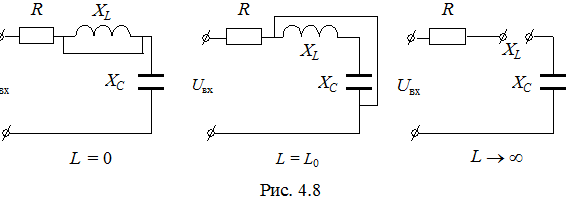Режим резонанса напряжений в RLC -цепи можно достигнуть, не только изменяя частоту, но и изменяя параметры индуктивности и емкости. Представим электрические схемы последовательного RLC -контура при L = 0, L = L0 (индуктивность достижения резонанса), L ® ¥ (рис. 4.8).
Значения I (L), UL (L), UC (L) для каждой схемы даны в табл. 4.1.
|
|
|
Таблица 4.1
| L |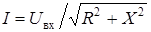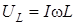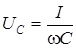 
| 
| 
|
| 
| ||
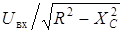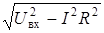| L 0 |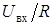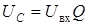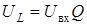 
| 
| 
|
| ¥ | U вх |
 |
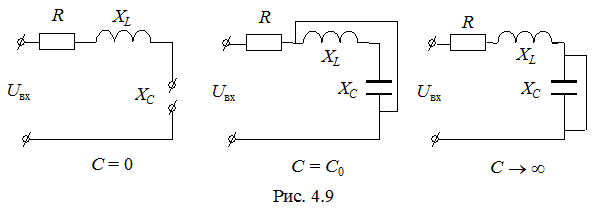Электрические схемы RLC -контура при С = 0, С = С 0(значение емкости при резонансе), С ® ¥ представлены на рис. 4.9.
Значения I (C), UL (C), UC (C) для каждой схемы даны в табл. 4.2.
Таблица 4.2
| C |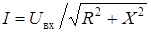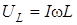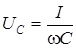 
| 
|
|
| U вх | |||
| C 0 |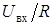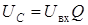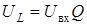
| 
|
|
| ¥ | 
|
|
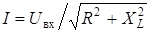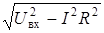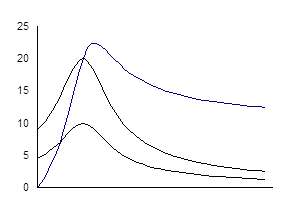
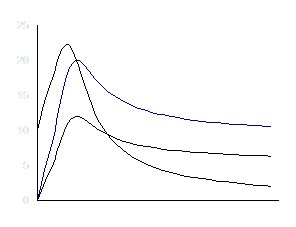
Характер изменения зависимостей I (L), UL (L), UC (L), I (C), UL (C), UC (C)представлен на рис. 4.10.
 
| 
|
