Классическое определение вероятности

Численная мера степени объективной возможности наступления события называется вероятностью события.

Пусть исходы некоторого испытания образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Такие исходы называются элементарными исходами, случаями или шансами.

Случай называется благоприятствующим (благоприятным) событию А, если появление этого случая влечет за собой появление события А.

Согласно классическому определению вероятность события А равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, т.е. Р(А)=m/n, где Р(А) – вероятность события А; m – число случаев, благоприятствующих событию А; n – общее число случаев.

Классическое определение (классическую формулу) вероятности следует рассматривать не как определение, а как метод вычисления вероятностей для испытаний, сводящихся к схеме случаев.

События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными.

Раздел1_2. Случайные величины, функции распределения, их свойства. Абсолютно непрерывные и дискретные распределения. Типовые распределения: биноминальное, пуассоновское, нормальное. Схема Бернулли и полиноминальная схема: основные формулы.

Случайной величиной называют величину, которая в результате испытаний примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Теоретико-множественная трактовка основных понятий теории вероятностей позволяет дать следующее определение случайной величины.

Случайной величиной Х называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий). Х = f(ω), где ω – элементарный исход (или элементарное событие, принадлежащее пространству Ω, т.е. ω ϵΩ).

Для дискретной случайной величины множество возможных значений случайной величины, т.е. функции f(ω), конечно или счетно, для непрерывной – бесконечно и несчетно.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

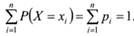Х х₁ х₂... х_n

p p₁ p₂... p_n

Для любой дискретной случайной величины

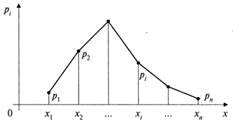Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат – соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей.

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х. F(x) = P(X<x)

Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х.

Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям величины и равны вероятностям этих значений. Сумма всех скачков функции F(x) равна 1.

Свойства функции распределения.

Свойство 1. Значения функции распределения принадлежат отрезку [0;1]: 0≤F(x)≤ 1.

Свойство 2. F(x) – неубывающая функция, т.е. F(x₂)≥F(x₁), если x₂>x₁.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a≤X<b) = F(b) – F(a).

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна 0.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a, b), то: 1) F(x)=0 при x≤a; 2) F(x) = 1 при x≥b.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

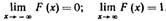
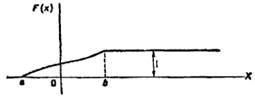Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.