Напряжения. Схема для принужденного (установившегося) режима представлена на рис.1.15

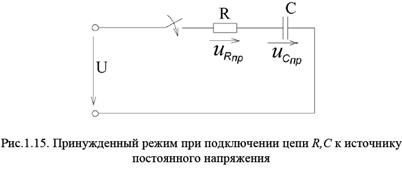
Схема для принужденного (установившегося) режима представлена на рис.1.15. К концу переходного процесса, когда конденсатор полностью зарядится, на нем устанавливается постоянное напряжение источника U. Действительно, для принужденного режима уравнение (1.27) имеет вид:

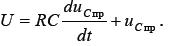
Так как 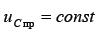, то из уравнения следует, что 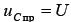. Ток в принужденном режиме (после заряда конденсатора до напряжения источника) будет равен нулю .

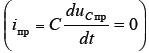Таким образом, переходное напряжение на емкости

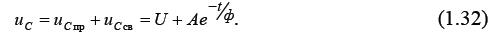
Для определения постоянной А используем независимое начальное условие. Согласно второму закону коммутации напряжение на емкости в момент включения выключателя остается таким же, как до коммутации. Если в исходном состоянии (до включения выключателя) конденсатор не был

заряжен, то .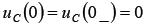

Для момента времени t=0 уравнение (1.32) имеет вид:

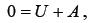откуда .

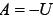Запишем окончательное выражение для переходного напряжения на емкости:

Ток и напряжение на R во время переходного процесса соответственно:

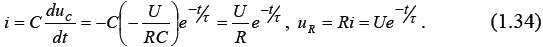
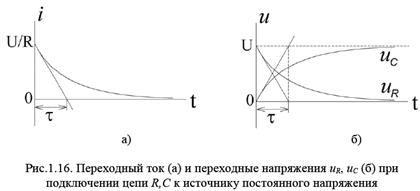
Графики переходного тока i и переходных напряжений представлены на рис.1.16.

Так как 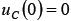, то при t=0 все напряжение источника приложено к активному сопротивлению 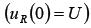, зарядный ток в цепи максимален 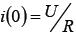. С течением времени в процессе заряда конденсатора C u возрастает, стремясь к напряжению источника U, а зарядный ток i уменьшается, стремясь к нулю. Чем больше постоянная времени 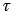, тем больше длительность переходного процесса. Через время 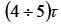переходный процесс практически заканчивается, т.е 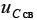затухает до значения, близкого к нулю.

Постоянная времени 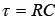может быть определена так же, как для цепи R, L, графически как подкасательная к кривой тока или напряжения 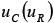в любой точке (например, при t=0).

Характер изменения напряжения на емкости и тока в данной цепи аналогичен соответственно закону изменения тока и напряжения на индуктивности при подключении цепи R, L к источнику постоянного напряжения.

Любая реальная электрическая цепь обладает некоторой паразитной индуктивностью, и ток в такой цепи не может возрастать скачком. Поэтому зарядный ток при подключении цепи R,C к источнику постоянногонапряжения будет нарастать от нуля до максимального значения при малых индуктивностях очень быстро, но не мгновенно, а затем начнет уменьшаться до нуля по экспоненте.

Следует отметить, что во время заряда конденсатора, при любом сочетании параметров R и C, всегда половина энергии, расходуемой источником за время переходного процесса, идет на накопление энергии в электрическом поле конденсатора, а другая – расходуется на тепло, выделяемое в активном сопротивлении.