Примером такой цепи может служить эквивалентная схема катушки индуктивности, обладающей активным сопротивлением R и индуктивностью L.
Дифференциальное уравнение такой цепи
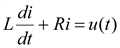 ,(9.4)
,(9.4)
где u(t) – напряжение на зажимах цепи.
Соответствующее однородное уравнение, определяющее свободный ток:
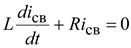 .
.
Lp + R = 0
имеет единственный корень p = –R/L. Тогда свободный ток можно вычислить как
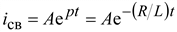 . (9.5)
. (9.5)
Выражение установившегося тока iу(t), являющегося частным решением дифференциального уравнения, определяемое видом заданной функции u(t).
Ток в переходном режиме
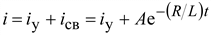 .
.
Постоянная интегрирования A определяется по начальному значению тока i.
Рассмотрим ряд частных случаев.
1. Пусть цепь в момент t = 0 отключается от источника и замыкается накоротко (рис. 9.1).
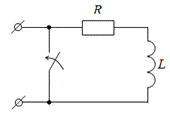
Рис. 9.1. Замыкание катушки индуктивности накоротко
После замыкания накоротко u = 0. Установившийся ток в этом случае iу = 0. Тогда полный ток
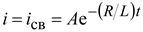 . (9.6)
. (9.6)
Начальное условие для определения A: i(0+) = i(0–).
Пусть к моменту коммутации ток в цепи был равен i(0–) = I. Следовательно, i(0+) = I. Полагая в уравнении (9.6) i = I и t = 0, находим I = A.
Решение уравнения имеет вид
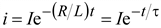 . (9.7)
. (9.7)
Величина τ = L/R имеет размерность времени и называется постоянной времени цепи. За промежуток времени t ток уменьшается в e раз. Чем больше τ, тем медленнее затухает ток.
Теоретически ток станет равным нулю через бесконечно большой промежуток времени, практически он становится малым за промежуток времени в несколько значений τ (рис. 9.2).
Постоянная времени τ равна длине подкасательной в любой точке кривой i(t) на рис. 9.2, так как 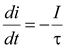 .
.
Энергия, выделяемая в виде теплоты в активном сопротивлении R, равна энергии, запасенной в магнитном поле цепи в начальный момент времени
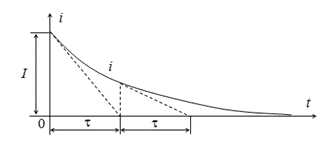
Рис. 9.2. Кривая изменения тока в катушке индуктивности
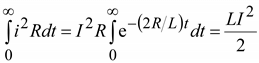 . (9.8)
. (9.8)
Постоянная времени τ больших катушек с сердечником может быть весьма значительной. Так, постоянная времени обмотки возбуждения крупных гидрогенераторов может иметь значение 5 с.
2. Рассмотрим процесс отключения от источника постоянного напряжения цепи, состоящей из индуктивной катушки с параметрами R и L и соединенной с ней параллельно ветви с сопротивлением R0(рис. 9.3).
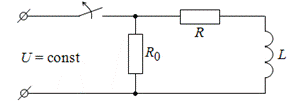
Рис. 9.3. Отключение катушки индуктивности
Переходный процесс описывается уравнением
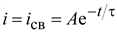 ,
,
где 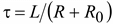 .
.
До размыкания рубильника в катушке протекает ток iL(0–) = U/R.
A = iL(0+) = iL(0–) = U/R.
Ток в катушке
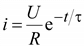 .(9.9)
.(9.9)
Напряжение на участке с сопротивлением R0 до размыкания было равно U, а в первый момент времени после размыкания оно окажется равным
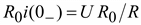 .(9.10)
.(9.10)
Если R0 > R, например, на зажимах катушки с сопротивлением R включен вольтметр с большим сопротивлением, то при отключении цепи напряжение на вольтметре в первый момент повысится R0/R раз.
Если энергия магнитного поля, запасенная в катушке достаточно велика, то вольтметр может быть сожжен. Поэтому во избежание возникновения больших перенапряжений при отключении цепей постоянного тока, обладающих большой индуктивностью, например, обмоток возбуждения генераторов, эти цепи предварительно замыкают на малое сопротивление.
3. Рассмотрим процессы при включении RL цепи на постоянное напряжение u = U = const (рис. 9.4).
Ток установившегося режима iу = U/R.
Общий ток в переходном режиме 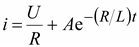 .
.
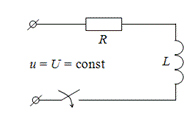
Рис. 9.4. Включение катушки индуктивности на постоянное напряжение
Если до включения ток был равен нулю i(0–) = 0, то при t = 0
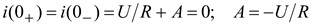 .
.
Решение уравнения
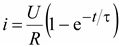 .(9.11)
.(9.11)
Напряжение на зажимах катушки
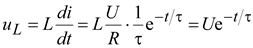 .(9.12)
.(9.12)
Кривые изменения тока и напряжения на катушке показаны на рис. 9.5.
4. Рассмотрим процесс при включении цепи под синусоидальное напряжение: 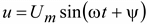 .
.
Ток установившегося режима
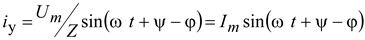 .
.
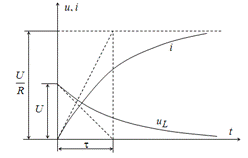
Рис. 9.5. Кривые изменения тока и напряжения
Общий ток 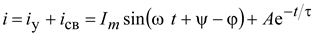 ,
,
где 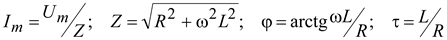 .
.
Постоянную интегрирования A определяем из начального условия i(0–) = 0.
i(0+) = i(0–) = Imsin(Ψ – j) + A = 0
Общий ток:
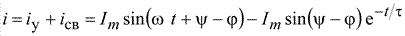 .(9.13)
.(9.13)
Кривые изменения тока и напряжения изображены на рис. 9.6.
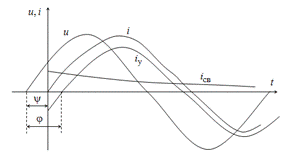
Рис. 9.6. Кривые изменения тока и напряжения при включении катушки на синусоидальное напряжение
Начальное значение свободного тока зависит от начальной фазы Ψ напряжения. Наибольшее значение свободного тока, равное амплитуде Im установившегося тока, имеет место, если Ψ – j = +π/2. Наибольшее значение результирующего тока не превышает двойной амплитуды установившегося тока. Свободный ток не возникает, и сразу наступает установившийся режим при условии Ψ = j.
31. Индуктивная катушка в цепи синусоидального тока
Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток 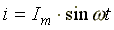 . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
. Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
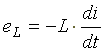 (6.9)
(6.9)
Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = eL = 0.
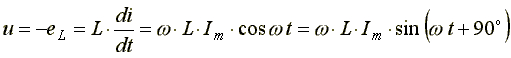 (6.10)
(6.10)
Таким образом, ток в индуктивности отстает по фазе от напряжения на 90o из-за явления самоиндукции.
Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:
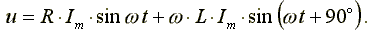 (6.11)
(6.11)
Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0o< φ < 90o), величина которого зависит от соотношения R и L. Выражение (6.11) в комплексной форме записи имеет вид:
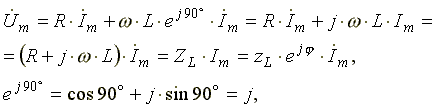 (6.12)
(6.12)
где ZL - полное комплексное сопротивление индуктивной катушки 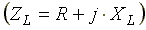 ;
;
ZL - модуль комплексного сопротивления;
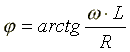 - начальная фаза комплексного сопротивления;
- начальная фаза комплексного сопротивления;
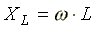 - индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
- индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
Полное сопротивление индуктивной катушки или модуль комплексного сопротивления
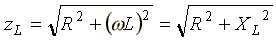 .
.
Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).
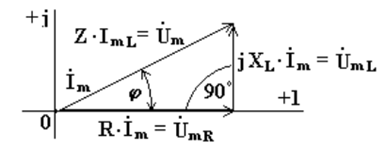
Рис. 6.5
Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90o.
В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений на величину тока Im, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).
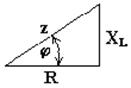 Из треугольника сопротивлений получим несколько формул:
Из треугольника сопротивлений получим несколько формул:
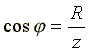 ;
; 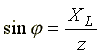 ;
;
Рис. 6.6
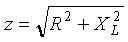 ;
;
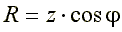 ;
; 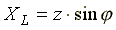 .
.
 2015-05-13
2015-05-13 4647
4647








