Дифференцирующим называется звено, которое описывается дифференциальным уравнением:
y=k 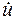 . (3.6)
. (3.6)
Его передаточная функция имеет вид:
W(p)=y(p)/u(p)=kp. (3.7)

|
Переходная характеристика дифференцирующего звена:
h(t)=k 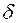 (t).
(t).

|
Рис. 3.5. Переходная характеристика звена
Импульсная переходная функция представляет собой «дуплет» 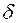 -функций
-функций
g(t)=k 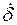 (t). (3.8)
(t). (3.8)
Рис. 3.6. Импульсная переходная характеристика
Получим теперь частотные характеристики звена.
АФХ: W(j 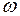 )=jk
)=jk 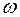 , совпадает с положительной мнимой полуосью на комплексной плоскости;
, совпадает с положительной мнимой полуосью на комплексной плоскости;
ВЧХ: R(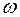 ) =0,
) =0,
МЧХ: I(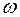 )=kw,
)=kw,
 АЧХ:
АЧХ: 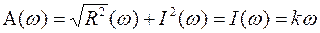 ,
,
ФЧХ: 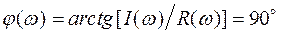 , т. е. на всех частотах звено имеет постоянный фазовый сдвиг;
, т. е. на всех частотах звено имеет постоянный фазовый сдвиг;
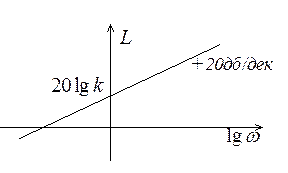
|
ЛАЧХ:
L(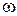 )=20lgk
)=20lgk 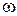 =20lgk+20lg
=20lgk+20lg 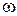 . (3.9)
. (3.9)
Как видно из графика рис. 3.7, дифференцирующее звено усиливает высокочастотные сигналы.
Рис. 3.7. ЛАЧХ дифференцирующего звена
 2015-05-13
2015-05-13 524
524








