(пропорционально - дифференцирующее)
Форсирующим называется звено, дифференциальное уравнение которого имеет вид
y=k1u+k2 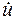 . (3.32)
. (3.32)
Как видим, его можно представить как сумму пропорционального и дифференцирующего звеньев.
Передаточная функция форсирующего звена,
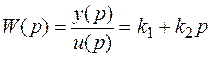 ,
,
записывается в стандартной форме
W(p)=k(1+Tp), (3.33)
где k 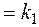 - коэффициент усиления, T=
- коэффициент усиления, T=  - постоянная времени звена.
- постоянная времени звена.
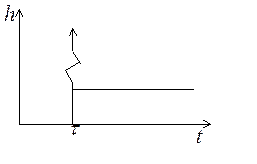 |
Вычислим его переходную характеристику
h(t- 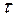 )=
)= 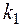 1 (t-
1 (t- 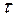 )+
)+  (t-
(t- 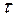 ) (3.34)
) (3.34)
и импульсную переходную функцию
g(t)= 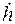 (t)=
(t)= 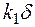 (t)+
(t)+  (t). (3.35)
(t). (3.35)
Рис. 3.18. Переходная характеристика
форсирующего звена
Запишем выражения для частотных характеристик.
АФХ: W(j 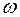 )=k(1+ j
)=k(1+ j 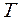
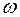 ); (3.36)
); (3.36)
ВЧХ: R(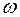 )=k;
)=k;
МЧХ: I(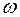 )=k
)=k 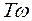 ;
;
АЧХ: A(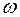 )=k
)=k 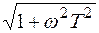 ;
;
ФЧХ: 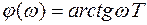 ;
; 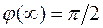 ; (3.37)
; (3.37)
ЛАЧХ: L(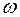 )=20lgk+10lg(1+T
)=20lgk+10lg(1+T 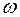 ). (3.38)
). (3.38)
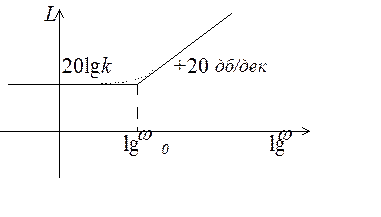 |
Асимптотическую ЛАЧХ форсирующего звена можно получить, рассматривая отдельно области низких и высоких частот, как в случае апериодического звена, или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.
Рис. 3.19. ЛАЧХ форсирующего звена
 |
Здесь 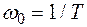 - собственная частота звена.
- собственная частота звена.
АФХ форсирующего звена строится по выражению (3.36) и имеет вид, представленный на рис. 3.20.
Рис. 3.20 АФХ форсирующего звена
 2015-05-13
2015-05-13 4572
4572








