Апериодическое звено

Апериодическим называется звено, дифференциальное уравнение которого имеет вид

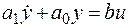. (3.17)

Перейдем к его стандартному описанию, для чего разделим обе части (3.17) на коэффициент a₀,

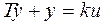, (3.18)

где 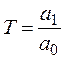- постоянная времени, 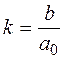- коэффициент передачи звена.

Заменив в (3.18) d/dt на p, перейдем к символической записи дифференциального уравнения,

(Tp+1)y = ku, (3.19)

и определим передаточную функцию апериодического звена:

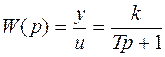. (3.20)

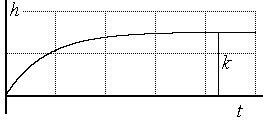Его переходную характеристику можно найти как решение уравнения (3.18) при u =1 (t) и y(0)=0,

h(t)=k( 1- 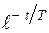)1(t). (3.21)

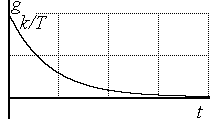Рис. 3.10. Переходная характеристика

Импульсную переходную функцию вычислим по соотношению:

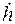g(t)= (t)= 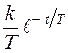. (3.22)

Рис. 3.11. Импульсная переходная функция

Для определения модальных характеристик запишем характеристическое уравнение звена

A(p)=Тр+1=0 (3.23)

и вычислим его корень, р=-1/Т.

Выражение, соответствующее АФХ апериодического звена, имеет вид:

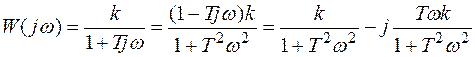. (3.24)

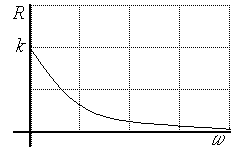Построим отдельно вещественную частотную характеристику по выражению

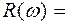
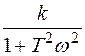. (3.25)

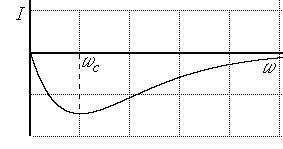Рис. 3.12. ВЧХ апериодического звена

Мнимую частотную характеристику апериодического звена строим по соотношению

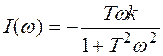. (3.26)

Рис. 3.13. МЧХ звена

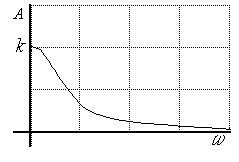Построим амплитудную частотную характеристику по выражению:

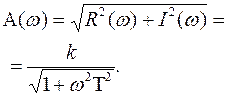(3.27)

Рис. 3.14. АЧХ апериодического звена

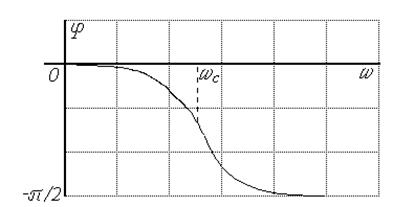ФЧХ звена определяется соотношением

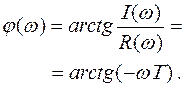
(3.28)

Рис. 3.15. ФЧХ апериодического звена

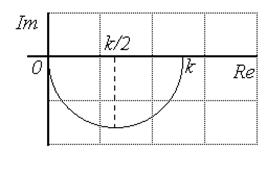На комплексной плоскости строим АФХ апериодического звена по выражению (3.24), которая имеет вид полуокружности и приведена на рис. 3.16.

Определим теперь логарифмическую амплитудную частотную характеристику в виде:

Рис. 3.16. АФХ апериодического звена

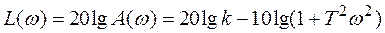. (3.29)

Наиболее просто можно построить асимптотическую ЛАЧХ. В этом случае рассматривают отдельно области высоких (ОВЧ) и низких частот (ОНЧ) и для каждой определяют свою асимптоту:

1) ОНЧ: 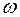<<1/T, L(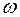)=20lgk. (3.30)

2) ОВЧ: 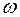>>1/T, L(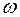)=20lgk-20lg(T 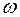). (3.31)

Частота 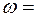1/T называется собственной частотой апериодического звена.

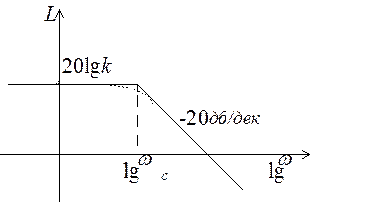На рис. 3.17 действительная ЛАЧХ показана пунктирной линией и несколько отличается от асимптотической, причем наибольшая погрешность будет на собственной частоте звена.

Рис. 3.17. ЛАЧХ апериодического звена