Модели вытеснения нефти

Рассмотрим модели процесса вытеснения нефти водой (газом).

3.1.2.1. Модель поршневого вытеснения. Предполагается движущийся в пласте вертикальный фронт, впереди которого нефтенасыщенность равна начальной (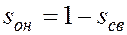), а позади остается промытая зона с остаточной нефтенасыщенностью 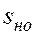. На рис. 25 схематически показан профиль насыщенности при

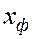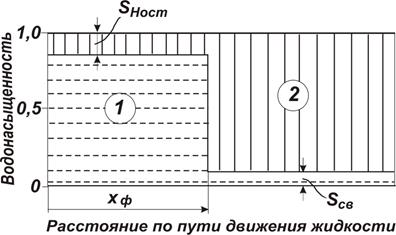
фиксированном положении фронта . Перед фронтом фильтруется только нефть, а позади – только вода.

Рис. 25. Модель поршневого вытеснения нефти водой.

Насыщенность: 1 – водой; 2 – нефтью

В соответствии с этой моделью полное обводнение продукции скважин должно произойти мгновенно в момент подхода фронта вытеснения к скважинам.

3.1.2.2. Модель непоршневого вытеснения (рис. 26). По схеме Бакли – Леверетта предполагается в пласте движущийся фронт вытеснения. Скачок нефтенасыщенности на нем значительно меньше, чем при поршневом вытеснении. Перед фронтом вытеснения движется только нефть, позади – одновременно нефть и вода со скоростями, пропорциональными соответствующим фазовым проницаемостям. Причем по мере продвижения фронта вытеснения скорости изменяются не только в зависимости от насыщенности в пласте, но и во времени. В момент подхода фронта к скважине происходит мгновенное обводнение до некоторого значения, соответствующего скачку нефтенасыщенности на фронте 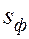, а затем обводненность медленно нарастает.

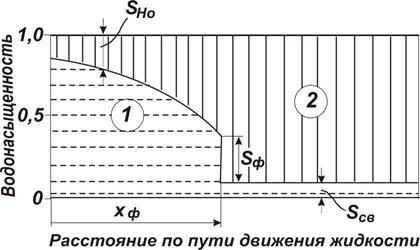Рис. 26. Модель непоршневого вытеснения нефти водой.

Насыщенность: 1– водой; 2 – нефтью

3.2. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

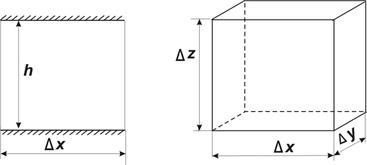
Выведем вначале уравнение неразрывности массы вещества при его одномерном прямолинейном движении в пласте. Масса 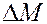вещества плотностью 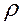в элементе пласта (рис. 27) длиной 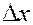, толщиной 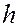и шириной 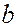, измеряемой в направлении, перпендикулярном к плоскости при пористости пласта 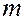, составит:

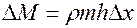. (3.11)

Если считать, что в элемент пласта через его левую грань поступает вещество с массовой скоростью 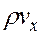, вытесняется из элемента с массовой скоростью и 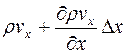, а накопленный объем его 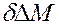за время 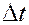получим с учетом того, что в элемент вошло больше вещества, чем из него вышло:

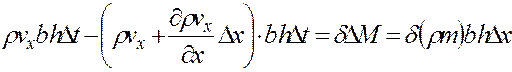. (3.12)

Из (3.12) имеем

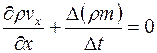. (3.13)

При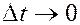

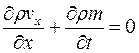. (3.14)

Уравнение (3.14) и есть уравнение неразрывности массы вещества в пласте при одномерном прямолинейном движении насыщающего его вещества. Чтобы получить такое уравнение для трехмерного случая, необходимо рассмотреть баланс массы в объемном элементе пласта 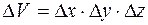(рис. 28). Рассматривая массовые скорости поступления вещества в куб и вытеснения из него, а также накопленный объем его в кубе, получаем:

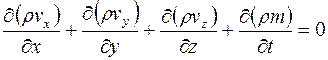. (3.15)

Уравнение (3.15) можно записать также в следующем общем виде:

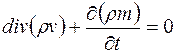. (3.16)

Уравнения (3.15), (3.16) – уравнения неразрывности массы вещества во время его движения при трехмерном измерении. Если в пласте одновременно движутся несколько веществ, находящихся как в газовой, так и в жидкой фазе, то составляют уравнения неразрывности массы каждого вещества (компонента) в соответствующих фазах.

3.3. УРАВНЕНИЕ ЭНЕРГИИ

Полная энергия единицы массы пласта 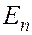состоит из отнесенных к единице массы внутренней удельной энергии пород пласта и насыщающих его веществ 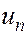, удельной потенциальной 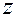и кинетической энергии веществ, движущихся в пласте со скоростью 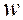. Поэтому

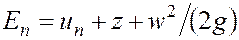. (3.17)

Из закона сохранения энергии или, точнее, из первого начала термодинамики следует, что изменение энергии пласта 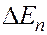и произведенной удельной работы 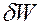равно количеству подведенного к пласту тепла 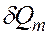,умноженного на механический эквивалент тепла 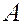, т. е.

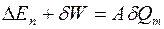, (3.18)

или с учетом (3.17)

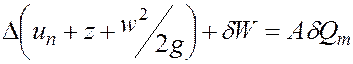. (3.19)

Дадим количественную оценку входящих в (3.19) величин. Удельная внутренняя энергия пласта 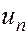при отсутствии в нем химических или ядерных превращений вещества представляет собой тепловую энергию в единице массы пласта, так что

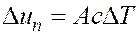, (3.20)

где 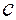– удельная теплоемкость пласта; Т – температура. Предположим, что пористый пласт насыщен водой 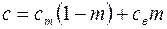( 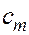– удельная теплоемкость пород пласта; 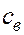- удельная теплоемкость воды, 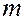– пористость). Пусть 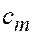= 1,046 кДж/(кг×К), 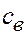= 4,184 кДж/(кг. К), 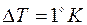, , 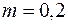тогда 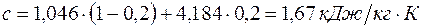, 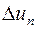=102×1,67×1=170 м. Удельная потенциальная энергия 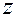в пластах может изменяться в соответствии с возможными изменениями уровня движущихся в пласте веществ. Обычно это десятки и иногда сотни метров.

Оценим возможные изменения удельной кинетической энергии. Скорость движения в пласте насыщающих его веществ изменяется в значительных пределах – от 0 до 10 м/сут = 3650 м/год = 1,16 ·10^-4 м/с. Сравнивая удельные потенциальную и кинетическую энергии пласта с его удельной внутренней энергией, необходимо учитывать, что выше вычислялась удельная внутренняя энергия пласта в целом, т. е. пород и насыщающих их веществ. Удельная потенциальная и удельная кинетическая энергия относятся только к насыщающим пласт веществам. Поэтому, с целью указанного сравнения, необходимо ввести коэффициент

,

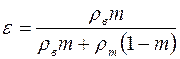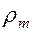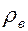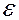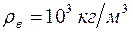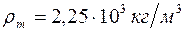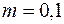
где – плотность горных пород; – плотность насыщающих пласт веществ, и умножать все виды удельной энергии, кроме внутренней, на . При , , 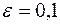. Тогда для изменения удельной кинетической энергии получим

.

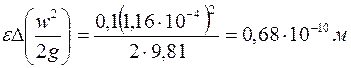Из приведенной оценки следует, что удельной кинетической энергией движущихся в пласте веществ можно всегда, кроме особых случаев движения веществ в призабойной зоне скважин, пренебречь.

Если изменение удельной потенциальной энергии движущегося в пласте вещества составляет даже 100 м, то при умножении этой величины на 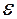получим 10 м. Изменение же температуры пласта всего на один градус равнозначно изменению удельной внутренней энергии почти на 200 м. Если разработка пласта ведется с использованием тепловых методов, то температура пласта может изменяться на сотни градусов, и его удельная внутренняя энергия станет преобладающей среди других видов энергии. Оценим возможную величину работы, которую могут производить насыщающие пласт вещества. Удельную работу 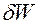, производимую насыщающим пласт веществом и отнесенную к единице массы вещества, определим следующим образом:

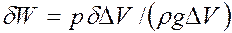, (3.21)

где 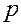– давление; 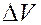– объем вещества, насыщающего пласт в элементарном объеме пласта; 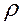– плотность этого вещества; 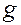– ускорение свободного падения.

Поровый объем пласта остается, вообще говоря, неизменным, поскольку не изменяются геометрия пласта и его пористость. Работа вещества в пласте связана всегда с его расширением. Поэтому в (3.21) и введена величина 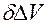, характеризующая расширение вещества. При этом условно можно считать, что вещество, насыщающее пласт, расширяясь, как бы выходит за пределы элементарного объема пласта. Будем считать, что при бесконечно малом расширении вещества в элементарном объеме пласта масса вещества 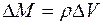остается неизменной, тогда

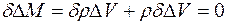и, следовательно,

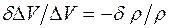. (3.22)

Подставляя (3.22) в (3.21), получаем:

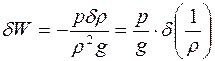. (3.23)

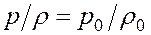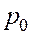Оценим возможную работу вещества, насыщающего пласт. Очевидно, что наибольшую работу может производить в пласте газ. Для простоты оценки будем считать газ идеальным, для которого , где и 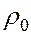– давление и плотность газа при начальных условиях. Отсюда для идеального газа

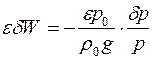. (3.24)

Пусть при снижении давления 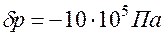, , 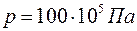, , 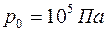, 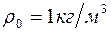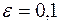тогда

.

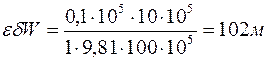Сделанная оценка показывает, что работа вещества, насыщающего пласт, хотя и намного меньше, чем изменение удельной внутренней энергии при тепловых методах разработки нефтяных месторождений, все же при определенных условиях, как это показывает опыт, может быть значительной.

Рассмотрим вопрос о том, чему равна входящая в (3.18) и (3.19) величина 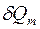. Тепловыделение в элементе пласта может происходить за счет экзотермических химических реакций и гидравлического трения и за счет теплопроводности. Уход тепла из элемента пласта за счет теплопроводности в дальнейшем будем учитывать при изменении внутренней энергии пласта 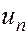. Перенос тепла из пласта в кровлю и подошву будем учитывать соответствующими граничными условиями, и поэтому в балансе энергии элементарного объема пласта его не будем принимать во внимание. Энергия движущегося в пористой среде вещества за счет гидравлического трения превращается в тепло. Для мощности гидравлического трения, отнесенной к единице массы движущегося вещества в элементе пласта, имеем следующее выражение:

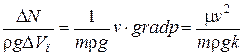. (3.25)

Допустим, что в пласте движется газ вязкостью 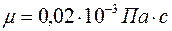со скоростью 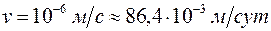. Проницаемость пласта 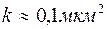, пористость 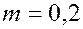, плотность газа 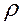при давлении 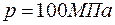составляет 100 кг/м³, тогда

.

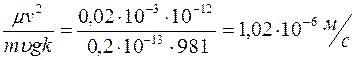В сутки из килограмма движущегося в пласте газа будет выделяться 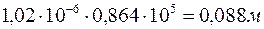энергии. Это – незначительная величина. Однако в призабойной зоне скважин скорость фильтрации того же газа может достигать 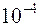м/с, а иногда и более. Тогда при тех же остальных условиях, что и выше, значение 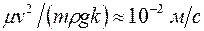. В сутки из килограмма фильтрующегося в пласте газа выделится энергии почти 9кДж. Таким образом, можно заключить, что наиболее существенное изменение энергии в элементе пласта связано с переносом тепла за счет теплопроводности и конвекции. Определенный вклад в энергетический баланс пласта, особенно при высоких скоростях движения насыщающих его веществ, вносят работа расширения-сжатия веществ и гидравлическое трение.

Напишем уравнение сохранения энергии в пласте, учитывая теплопроводность и конвекцию, а также работу расширения-сжатия веществ и гидравлическое трение.

Рассматривая, как и при выводе уравнения неразрывности массы фильтрующегося в пласте вещества, поток внутренней энергии 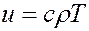и энергии сжатия 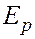, а также считая, что тепло поступает в элементарный объем только за счет гидравлического трения, т. е. что 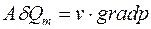, получаем:

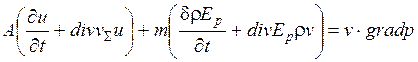. (3.26)

Здесь 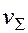– вектор суммарной скорости теплопереноса в пласте за счет теплопроводности и конвекции, 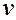– вектор скорости фильтрации. Выражение (3.26) и есть дифференциальное уравнение сохранения энергии в пласте, выведенное при указанных выше предположениях.