Внутренние силовые факторы при ППИ

Понятие об изгибающем моменте и поперечной силе

Простая балка КВ находится в состоянии плоского поперечного изгиба (рис.4.9). Определим внутренние усилия, возникающие в произвольном сечении балки, расположенном на расстоянии х от левой опоры.

Используем систему координат: ось х – вдоль оси балки; ось у – в плоскости симметрии балки, вниз; ось z – перпендикулярно плоскости симметрии.

Поскольку в случае использования метода сечений система внешних сил должна быть полной, перед определением внутренних усилий необходимо определить реакции опор. С этой целью используем систему уравнений равновесия для плоской системы. Из уравнения 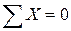получим .

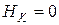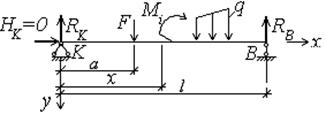
Рис.4.9

Отметим, что опорная реакция, направленная вдоль оси стержня, при плоском поперечном изгибе не возникает, что обусловлено отсутствием у рассматриваемой деформации составляющих активной внешней нагрузки, действующих вдоль оси х.

Вертикальные реакции определяем из уравнений равновесия для моментов внешних сил

Уравнение 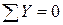используем для проверки правильности определения опорных реакций.

Для определения внутренних усилий применяем метод сечений.

В сечении балки действует плоская система распределенных сил с интенсивностью 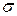и 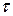. Равнодействующими этих сил могут быть только три внутренних усилия: нормальная (продольная) сила – N, поперечная (перерезывающая) сила – Q_y, изгибающий момент – M_z. Поскольку при плоском поперечном изгибе составляющие внешней сил вдоль оси х отсутствуют, отсутствует также в сечении балки нормальная сила (N = 0).

Таким образом, при плоском поперечном изгибе в сечении балки возникают поперечная сила Q и изгибающий момент M (здесь и далее при исследовании рассматриваемой деформации индексы у внутренних усилий будем опускать).

Очевидно, что:

поперечная сила Q является равнодействующей касательных напряжений 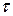, действующих в сечении в направлении у;

изгибающий момент M является равнодействующей, нормальных напряжений 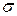относительно оси, лежащей в плоскости сечения и перпендикулярной плоскости симметрии балки.

Примем для Q и M следующее правило знаков (рис.4.10):

поперечная сила Q – положительна, если стремится развернуть ближайший к ней элемент по ходу часовой стрелки;

изгибающий момент M – положителен, если приводит к сжатию верхних волокон балки.

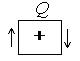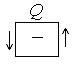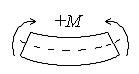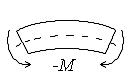Рис.4.10

Определим внутренние силы Q и M в произвольном сечении на расстоянии х от левой опоры. Для этого выделим, согласно методу сечений, левую часть балки, заменив отброшенную ее часть положительными внутренними силами Q и M (рис.4.11).

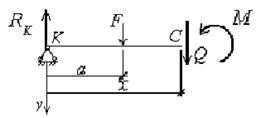
Рис.4.11

Для определения поперечной силы Q запишем условие равновесия отсеченной левой части балки для сил

Из этого уравнения получим

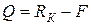Очевидно, что правая часть уравнения представляет собой алгебраическую сумму всех внешних сил, расположенных слева от сечения. На основании этого можно записать

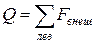Заметим, что в эту сумму со знаком «+» входит внешняя сила R_К, а со знаком «-» – сила F. Поскольку внутреннее усилие Q на расчетной схеме положительно, можно установить на основе знаков для R_К и F правило знаков для внешней силы, входящей в сумму : знак внешней силы положительный, если сила стремится повернуть рассматриваемый элемент балки относительно сечения по ходу часовой стрелки.

Очевидно, что аналогичный результат получим, рассматривая правую часть балки (естественно, что в этом случае в сумму 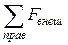войдет равнодействующая распределенной нагрузки).

Таким образом, можно записать

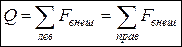, (4.1)

т.е. поперечная сила в сечении равна алгебраической сумме всех внешних сил, расположенных по одну сторону от сечения, причем внешняя сила считается положительной, если стремится повернуть рассматриваемый элемент балки относительно сечения по ходу часовой стрелки.

Для определения в сечении изгибающего момента M запишем для левой части балки уравнение равновесия моментов относительно сечения (точки С)

откуда получим

Правая часть уравнения представляет собой алгебраическую сумму моментов всех внешних сил, расположенных слева от сечения, т.е.

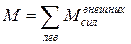При положительном изгибающем моменте M в правую часть полученной формулы со знаком «+» вошел момент от внешней силы R_К, который способствует сжатию верхних волокон балки (момент от силы F верхние волокна растягивает). Отсюда вытекает правило знака для момента внешней силы: момент от внешней силы положителен, если приводит к сжатию верхних волокон балки.

Аналогичный результат получим, рассматривая правую часть балки. В этом случае, наряду с моментом от силы R_B, в сумму 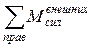войдет сосредоточенный внешний момент M_i, а также момент от распределенной нагрузки.

Исходя из вышеизложенного, запишем

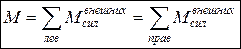, (4.2)

т.е. изгибающий момент в сечении равен алгебраической сумме моментов всех внешних сил, расположенных по одну сторону от сечения относительно сечения, причем момент от внешней силы считается положительным, если вызывает сжатие верхних волокон балки.

Дифференциальные соотношения между q, Q и M

(теоремы Д.И.Журавского)

Простая балка КВ находится в состоянии плоского поперечного изгиба. Выделим на участке действия распределенной нагрузки, интенсивность которой q = q (х), элемент длиной dx и рассмотрим его равновесие под действием внешней нагрузки и внутренних усилий (рис.4.12). Внутренние силы задаем положительными. Из-за малости длины элемента полагаем, что по его длине нагрузка распределена равномерно (q=const). Заметим, что, поскольку при переходе от левого сечения элемента к правому независимая переменная х получила бесконечно малое приращение dx, изгибающий момент M и поперечная сила Q, как функции, также получат малые приращения dM и dQ.

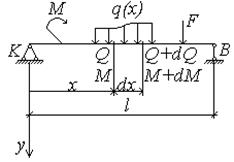
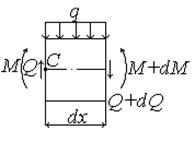
Рис.4.12

Условие равновесия для сил, действующих на элемент балки, имеет вид

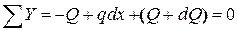, откуда 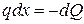, либо в другой форме

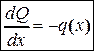, (4.I)

т.е. производная от поперечной силы равна интенсивности распределенной нагрузки с обратным знаком. Эту формулу называют первым дифференциальным соотношением теории изгиба балок либо первой теоремой Журавского.

Запишем уравнение равновесия для моментов относительно центра тяжести левого сечения (точки С)

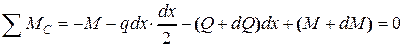откуда, приводя подобные члены и отбрасывая член второго порядка малости, будем иметь

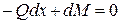Из этого уравнения получим второе дифференциальное соотношение Журавского, согласно которому производная от изгибающего момента в сечении равна поперечной силе в этом сечении

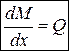. (4.II)

Подстановка (4.II) в (4.I) даст третье дифференциальное соотношение Журавского: вторая производная от изгибающего момента в сечении равна интенсивности поперечной нагрузки в этом сечении (с обратным знаком)

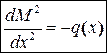. (4.III)

Некоторые замечания

Можно утверждать следующее:

1) наибольшие по абсолютной величине нормальные напряжения max│ s │ возникают в сечении, в котором изгибающий момент достигает максимального по абсолютной величине значения (M = max│ M │);

2) наибольшие по абсолютной величине касательные напряжения max│ t │ отмечается в сечении, в котором максимального по абсолютной величине значения достигает поперечная сила (Q = max│ Q │).

Сечения, в которых M = max│ M │ либо Q = max│ Q │, называются опасными. С целью отыскания положения опасных сечений строятся эпюры Q и M: графические изображения распределения Q и M по длине балки.