Доказательства приведенных ниже правил построения эпюр Q и М предлагается выполнить студентам самостоятельно.
1. Если на участке балки q = 0, то Q = const (прямая, параллельная к базе), а M будет изменяться по линейному закону (прямая, наклонная к базе).
2. Если на участке балки действует q = q 0 = const, то Q изменяется на участке по линейному закону, а М – по закону квадратной параболы (рис.4.13).
3. Если на участке балки Q плавно меняет знак, то на этом участке будет отмечаться экстремум для М. Причем экстремальное значение М достигается в сечении, где Q = 0 (рис.4.13).
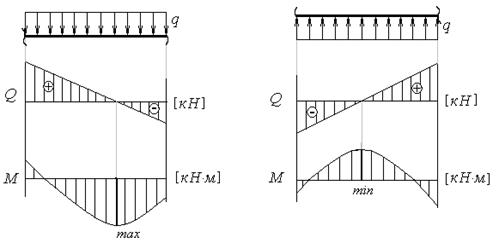
Рис.4.13 (к пунктам 2, 3, 4)
4. Если Q > 0, то, при рассмотрении балки слева направо, M, в алгебраическом смысле, возрастает (эпюра M уходит вниз), если Q < 0, M убывает (эпюра М уходит вверх). Отсюда следует, что при смене знака Q на участке с (+) на (–) изгибающий момент M в алгебраическом смысле достигает максимального значения; при смене знака с (–) на (+) изгибающий момент достигает минимального значения (рис.4.13).
5. Внешняя сосредоточенная сила в сечении на эпюре Q отражается в виде скачка на величину силы, в соответствии с ее направлением, а на эпюре М в виде излома с острием, направленным в сторону силы (рис.4.14).
6. Сосредоточенный внешний изгибающий момент на эпюре Q не отражается, а на эпюре М отражается в виде скачка на величину момента, в соответствии с его направлением (рис.4.14).
7. Начало (конец) распределенной нагрузки на эпюре Q отражается виде излома, а на эпюре М в виде плавного перехода от прямой к кривой (и наоборот) (рис.4.15).
8. Выпуклость кривой, ограничивающей эпюру М, направлена в соответствии с направлениями распределении нагрузки (рис.4.15).
9. Если концевые сечения балки свободны от внешней активной или реактивной нагрузки, то Q и М в этих сечениях равны нулю. При наличии внешней активной нагрузки или реакции Q и М в этих сечениях должны соответствовать внешним силовым факторам.
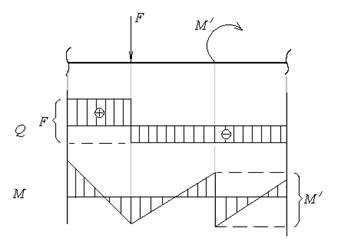 | 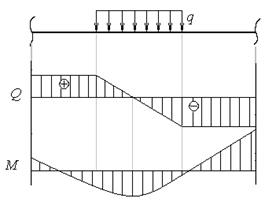 |
| Рис.4.14 (к пунктам 5 и 6) | Рис.4.15 (к пунктам 7 и 8) |
Пункты с 4 по 9 справедливы только для принятого правила знаков при построении эпюр слева направо.
Чистый плоский изгиб. Формула для s
Чистый плоский изгиб – такой случай плоского изгиба, когда на участке балки Q = 0, а M = const (при отсутствии нагрузки в виде распределенного по длине момента).
Построим для простой балки КВ эпюры Q и M (см. рис.4.16). Анализ эпюр показывает, что второй участок балки находится в состоянии чистого изгиба (Q= 0; M=const). Очевидно, что в сечениях балки на этом участке будут возникать только нормальные напряжения s (t = 0).
Определим нормальные напряжения s, действующие в сечениях участка чистого изгиба балки.
Напомним, что задача определения напряжений является внутренне статически неопределимой. Поэтому для ее решения необходимо привлекать соображения, связанные с деформацией балки. Эти соображения отражаются гипотезами и допущениями, которые использует сопротивление материалов при построении расчетных моделей. В частности, для определения деформаций и нормальных напряжений s при чистом изгибе балки используем следующие гипотезы и допущения:
1) гипотезу плоских сечений Я.Бернулли: сечения плоские и перпендикулярные к оси балки до деформации остаются плоскими и перпендикулярными к оси после деформации;
2) продольные волокна балки не надавливают друг на друга;
3) материал балки подчиняется закону Гука, причем модуль Юнга Е одинаков при растяжении и сжатии.
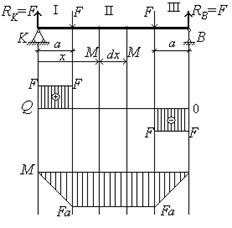
Рис.4.16
Рассмотрим вначале геометрическую сторону задачи. Предварительно введем ряд новых понятий, связанных с особенностями деформации при изгибе балок:
- нейтральное волокно – волокно балки, которое не испытывает продольные деформации при изгибе, а только искривляется;
- нейтральный слой – совокупность нейтральных волокон по ширине балки;
- нейтральная ось (н.о.) – линия пересечения нейтрального слоя с силовой плоскостью (плоскостью симметрии) балки;
- нейтральная линия (н.л.) – линия пересечения нейтрального слоя с плоскостью сечения балки.
 На участке чистого изгиба выделим элемент балки длиной dx и изобразим его в исходном и деформированном состоянии (рис.4.17). Введем нейтральную ось – н.о. (отрезок ав).
На участке чистого изгиба выделим элемент балки длиной dx и изобразим его в исходном и деформированном состоянии (рис.4.17). Введем нейтральную ось – н.о. (отрезок ав).
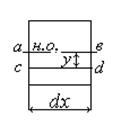
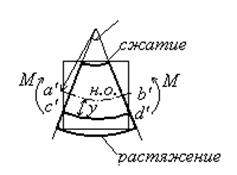
элемент в исходном элемент в деформированном
состоянии состоянии
Рис.4.17
Деформированный элемент изображаем в соответствие с гипотезой плоских сечений Я.Бернулли. При этом обозначим: r – радиус кривизны нейтральной оси; dq – угол взаимного поворота сечений балки.
Определим деформацию произвольного волокна балки cd, которое расположено на расстоянии y от нейтральной оси
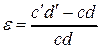 .
.
Здесь: cd – исходная длина волокна, c¢d¢ – длина этого волокна после деформации. Очевидно, что 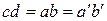 , где a¢b¢ – длина отрезка искривленной нейтральной оси. Длину этого отрезка можно определить по формуле
, где a¢b¢ – длина отрезка искривленной нейтральной оси. Длину этого отрезка можно определить по формуле 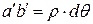 (см. рис). Поскольку
(см. рис). Поскольку 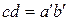 , исходную длину рассматриваемого волокна представим в виде
, исходную длину рассматриваемого волокна представим в виде 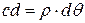 , а длину после деформации – в виде
, а длину после деформации – в виде 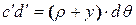 . Подставляя эти выражения в формулу для e, получим
. Подставляя эти выражения в формулу для e, получим
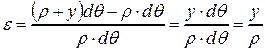 .
.
Таким образом, деформация произвольного волокна, расположенного на расстоянии у от нейтральной оси, определяется по формуле
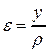 . (4.3)
. (4.3)
Физическая сторона задачи. Согласно допущению о ненадавливании продольных волокон друг на друга, рассматриваемое отдельное волокно находится в линейном напряженном состоянии, и закон Гука для него имеет вид
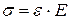 .
.
Подставляя в эту формулу выражение (3), получим
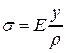 . (4.4)
. (4.4)
Формулу (4.4), однако, использовать для определения напряжения s нельзя, поскольку неизвестно положение нейтральной оси, от которой задается расстояние до рассматриваемого произвольного волокна – у, а также неизвестна величина радиуса кривизны нейтральной оси – r.
Рассмотрим, в этой связи, равновесие выделенного элемента балки (статическая сторона задачи) (рис.4.18). Причем к левому сечению элемента приложим, изгибающий момент М, а в правом сечении представим этот момент напряжениями s. Для этого введем в сечении систему координат: ось x – нейтральная ось балки, ось y – ось симметрии сечения, ось z - нейтральная линия сечения балки. Выделим бесконечно малую площадку dA с положительными координатами y и z и приложим к этой площадке положительные нормальные напряжения s, соответствующие положительному моменту М. Тогда элементарная нормальная сила, действующая по площадке dA, будет равна s×dA, а элементарные моменты относительно осей у и z соответственно составят dMy = s×dA×z и dMz = s dA×y.
Силы, действующие на элемент балки, представляют собой пространственную систему. Очевидно, что из шести уравнений равновесия для рассматриваемой пространственной системы три уравнения являются тождествами
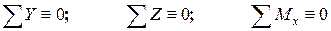 .
.
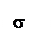
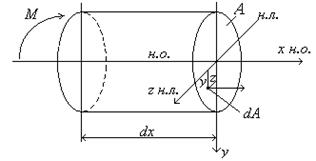
Рис.4.18
Рассмотрим оставшиеся уравнения равновесия.
В уравнение равновесия 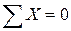 войдет только равнодействующая нормальных напряжений, приложенных к правому сечению элемента, которую определим путем суммирования (интегрирования) элементарных сил s×dA по площади сечения А. Рассматриваемое уравнение равновесия при этом примет вид
войдет только равнодействующая нормальных напряжений, приложенных к правому сечению элемента, которую определим путем суммирования (интегрирования) элементарных сил s×dA по площади сечения А. Рассматриваемое уравнение равновесия при этом примет вид
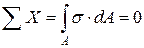 .
.
Подставляя в это уравнение соотношение (4) и вынося за знак интеграла величины, которые не зависят от переменной интегрирования, будем иметь
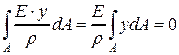 .
.
Поскольку 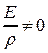 , получаем
, получаем 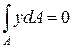 . С другой стороны,
. С другой стороны, 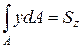 , где Sz – статический момент сечения относительно оси z. Таким образом, из рассмотренного уравнения равновесия следует, что в принятой системе координат Sz =0.
, где Sz – статический момент сечения относительно оси z. Таким образом, из рассмотренного уравнения равновесия следует, что в принятой системе координат Sz =0.
Запишем сумму моментов относительно оси у, суммируя (интегрируя) элементарные моменты dMy по площади сечения
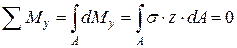 .
.
Используя подстановку (4), получим
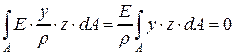 .
.
В этом уравнении 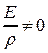 , тогда
, тогда 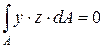 . Но
. Но 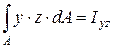 , где Iyz – центробежный момент инерции сечения относительно осей y и z. Отсюда следует, что центробежный момент инерции относительно осей y и z равен нулю (
, где Iyz – центробежный момент инерции сечения относительно осей y и z. Отсюда следует, что центробежный момент инерции относительно осей y и z равен нулю (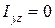 ).
).
На основе полученных выше соотношений (Sz =0 и 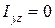 ) можно сделать следующие важные выводы:
) можно сделать следующие важные выводы:
1) ось z, совпадающая с нейтральной линией, является главной центральной осью поперечного сечения балки, т.е. при чистом плоском изгибе нейтральная линия совпадает с главной центральной осью сечения;
2) ось х, совпадающая с нейтральной осью балки, является ее геометрической осью, т.е. при чистом плоском изгибе нейтральная ось совпадает с геометрической осью балки.
Последнее уравнение равновесия для выделенного элемента будет включать в себя изгибающий момент, приложенный к левому сечению, и момент, обусловленный нормальными напряжениями, полученный путем суммирования элементарных моментов dMz
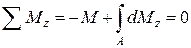 .
.
Из этого уравнения, с учетом (4.4), получим
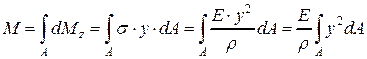 .
.
Здесь 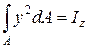 – момент инерции сечения относительно главной центральной оси z. Подставляя его в выражение для изгибающего момента, будем иметь
– момент инерции сечения относительно главной центральной оси z. Подставляя его в выражение для изгибающего момента, будем иметь
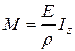 .
.
Отсюда получаем формулу для кривизны оси балки
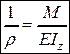 . (4.5)
. (4.5)
Здесь: произведение 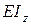 называют жесткостью сечения балки при изгибе.
называют жесткостью сечения балки при изгибе.
Из (4.5) следует, что при чистом изгибе ось балки будет искривляться по дуге окружности с радиусом r.
Синтезируя результаты, полученные на разных этапах решения задачи, подставим (4.5) в (4.4)
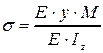 ,
,
откуда получим формулу для нормальных напряжений s при чистом изгибе
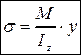 . (4.6)
. (4.6)
Здесь: М – изгибающий момент в сечении балки;
Iz – момент инерции сечения относительно главной центральной оси z;
y – координата точки, в которой определяется s (расстояние от оси z с соответствующим знаком).
Из формулы (4.6) следует, что s по ширине сечения не изменяется, а по высоте сечения изменяется по линейному закону.
Некоторые важные замечания
Полученная для нормальных напряжений формула (4.6) при чистом изгибе является точной (поскольку точно выполняется гипотеза плоских сечений Я.Бернулли). Об этом свидетельствуют результаты расчета s методами теории упругости, которые не используют гипотезу Я.Бернулли, а также данные экспериментов.
В случае плоского поперечного изгиба касательные напряжения, возникающие, согласно закону парности, в продольных сечениях балки, параллельных координатной плоскости x - z, приводят к тому, что гипотеза Я.Бернулли не выполняется (поперечные сечения искривляются). Это обусловливает погрешности при определении s по формуле (4.6), однако для балок длинных и средней длины указанная погрешность не превышает (3-5)%. Поэтому формулу (4.6) применяют также и при плоском поперечном изгибе, при котором изгибающий момент изменяется по длине балки. При этом остаются в силе выводы, касающиеся совпадения нейтральной оси с геометрической осью балки и нейтральной линии с главной центральной осью инерции поперечного сечения балки.
 2015-05-13
2015-05-13 1546
1546








