2015-05-13
1173
I. Бисимметричные (с двумя осями симметрии) сечения балки
Построим для прямоугольного, двутаврового и кругового сечений балки эпюру s, используя формулу для нормальных напряжений (4.6), полагая при этом, что изгибающий момент в рассматриваемом сечении положительный (М >0). Очевидно, что при разных значениях напряжений эпюры s будут иметь одинаковый вид (форму) (см. рис.4.19).
Из приведенной эпюры s видно, что максимальные по абсолютной величине напряжения в области растяжения и сжатия одинаковы и действуют в точках, наиболее удаленных от оси, при y =maxç y ç.
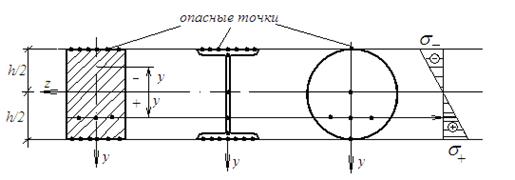
Рис.4.19
Используя подстановку y =maxç y ç, получим по формуле (4.6) максимальные напряжения в заданном сечении
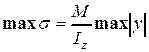, либо 
.
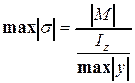В последней формуле знаменатель
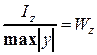
представляет собой момент сопротивления сечения балки относительно оси z. Таким образом, с учетом этого, максимальные напряжения в заданном произвольном сечении балки будут определяться по формуле
.
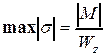Точки, в которых возникают наибольшие по абсолютной величине напряжения, называются опасными.
Условие прочности записывают для наиболее напряженной точки балки. Этой точкой является опасная точка в опасном сечении.
Поскольку опасное сечение балки располагается там, где изгибающий момент по абсолютной величине максимален (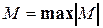
), напряжения в наиболее напряженной точке будут равны
,
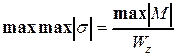а условие прочности по нормальным напряжениям при плоском поперечном изгибе примет вид
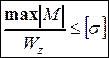. (4.7)
Это условие прочности записано для материала, который одинаково работает на растяжение и сжатие. Если материал по разному сопротивляется растяжению и сжатию ([s-] ≠ [s+]) необходимо записывать только условие прочности с меньшим значением допускаемого напряжения [s]. Как правило, это условие прочности для точки с растягивающими напряжениями (для [s+])
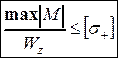. (4.8)
II. Сечения балки с одной осью симметрии
(на примере таврового профиля)
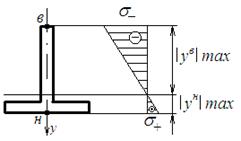
Рис.4.20
Из эпюры видно, что в этом случае максимальные растягивающие и сжимающие напряжения в сечении различные.
Условие прочности для материалов одинаково работающих на растяжение-сжатие будет иметь вид (4.7). В случае если материал не одинаково сопротивляется растяжению и сжатию, условие прочности необходимо формулировать для двух точек:
- точки опасной по растяжению (точка н),
- точки опасной по сжатию (точка в)
; 
.
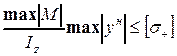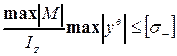Заметим, что для балок, сечение которых имеет одну ось симметрии, выполненных из материалов по разному сопротивляющихся растяжению и сжатию (например, выполненных из бетона), в зависимости от схемы их нагружения и закрепления необходимо решать вопрос об ориентации сечения (полка сверху либо полка снизу). Подумайте об этом.
