Дифференциальное уравнение упругой линии (изогнутой оси) балки

Рассмотрим деформацию консольной балки, нагруженной на свободном краю силой F (рис.4.31).

Плоская кривая, форму которой приобретает ось балки при деформации плоского изгиба, называется упругой линией балки (искривленной осью).

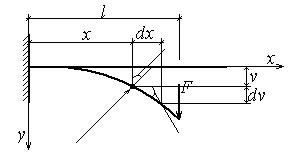
Рис.4.31

При плоском изгибе деформация оси балки полностью характеризует деформацию балки в целом. К характеристикам деформации балок относятся (рис.4.31):

- прогиб балки (n) – вертикальные смещения точек оси или, иначе, смещения точек оси, перпендикулярные к ее исходному положению. Поскольку мы рассматриваем малые перемещения, прогиб считаем также малым (горизонтальными или, иначе, продольными смещениями точек оси при этом пренебрегаем).

- угол поворота сечения (q) – угол, на который разворачивается рассматриваемое сечение балки при деформации. Этот угол, согласно гипотезе Я.Бернулли, равен углу между касательной к упругой линии в заданном сечении и недеформированной осью.

Правило знаков для n и q:

- прогиб – положительный вниз (отрицательный вверх);

- угол поворота сечения – положительный по ходу часовой стрелки.