Уравнение упругой линии балки

Установим связь между характеристиками деформаций и внутренними усилиями, возникающими в сечении балки при плоском поперечном изгибе. Предварительно отметим, что для рассматриваемых балок средней и большой длины (l >5 h) решающим фактором при определении деформаций является изгибающий момент М. Вклад поперечной силы Q при этом пренебрежимо мал, однако он увеличивается при уменьшении длины балки, и для коротких балок поперечная сила должна учитываться в расчетах. Рассматриваем, как и ранее балки средней длины и длинные.

Напомним, что при выводе формулы для s при чистом плоском изгибе было получено соотношение между кривизной оси балки (1/ r ) и изгибающим моментом в сечении (формула 4.5)

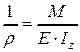, (4.5)

где 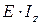– изгибная жесткость сечения балки.

В дифференциальной геометрии выражение для кривизны плоской кривой имеет вид:

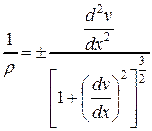(4.15)

Подставляя (4.15) в (4.5), получим связь между прогибом и изгибающим моментом

.

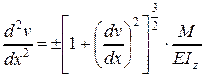Знак в этой формуле определяется в зависимости от знака изгибающего момента и знака кривизны: если знаки момента и кривизны одинаковы – в формуле знак «+», если разные – знак «-». Заметим, что знак кривизны определяется используемой системой координат, знак же изгибающего момента от направления координатных осей не зависит, а определяется согласно характеру деформаций нижних и верхних волокон балки. В этой связи, ниже, на рис.4.33 в различных системах координат для участков балки с положительными и отрицательными изгибающими моментами приведены знаки кривизны оси.

В системе координат, которую мы используем в расчетах (система 1), знаки моментов и кривизны для деформированных осей балок различны, поэтому в рассматриваемом уравнении принимаем знак «-»

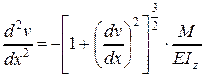. (4.16)

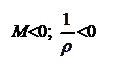
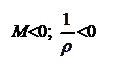
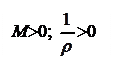
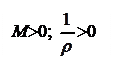
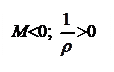
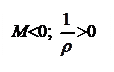
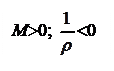
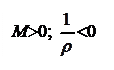
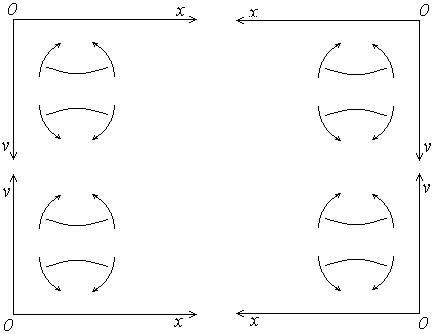
Рис.4.33

Уравнение (4.16) является точным уравнением упругой линии балки. Это дифференциальное уравнение второго порядка, обыкновенное, неоднородное, нелинейное. Нелинейность приводит к определенным трудностям решения такого уравнения. Однако, поскольку мы рассматриваем малые перемещения и малые углы поворота сечений 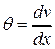, квадратом угла поворота 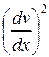, по сравнению с единицей, можно пренебречь. Тогда уравнение (16) примет вид

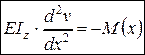(4.17)

Это уравнение и является искомым дифференциальным уравнением упругой линии балки при рассматриваемых малых ее перемещениях. В отличие от уравнения (4.16), оно является линейным, допускает разделение переменных и легко интегрируется (решается).

На основе дифференциального уравнения упругой линии балки можно определять основные характеристики деформаций: прогиб n и угол поворота q произвольного сечения балки. При этом используются два метода:

1) метод непосредственного интегрирования уравнения (4.17);

2) метод начальных параметров.