2015-05-13
527
Дифференциальное уравнение упругой линии балки на определенном i ее участке (i – номер участка) имеет вид
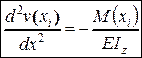. (4.18)
Здесь: v (i) и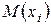 
– прогиб балки и выражение для изгибающего момента на i -том участке балки.
Для определения прогиба и угла поворота произвольного сечения балки методом непосредственного интегрирования уравнения (4.18) необходимо на каждом участке балки записать в принятой системе координат аналитическое выражение для изгибающего момента в форме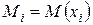 
, затем, подставляя полученные выражения в (4.18) и разделяя переменные, дважды интегрировать каждое уравнение.
Для балки с постоянной жесткостью сечения (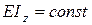
) получим:
- в результате первого интегрирования
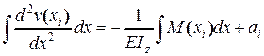, откуда 
;
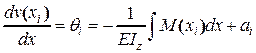- в результате второго интегрирования
,
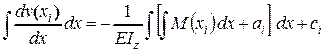откуда будем иметь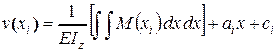 
.
В полученных соотношениях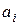 
и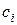 
– постоянные интегрирования, которые определяются из условий на границах участка. Очевидно, что для определения значени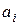й и 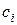необходимо сформулировать на каждом участке по два условия.
