II. Метод начальных параметров

Метод начальных параметров предполагает определение только двух постоянных (при решении задач этим методом необходимо решать систему максимум двух уравнений с двумя неизвестными).

Метод базируется на следующих положениях:

1. Начало координат размещается на левом краю балки и выражения для изгибающих моментов при выводе формул метода записывается только по левым силам.

2. Если распределенная нагрузка заканчивается не на правом краю балки, то она продлевается до этого края, а для того, чтобы условия нагружения не изменялись, вводится компенсирующая нагрузка той же интенсивности противоположного направления.

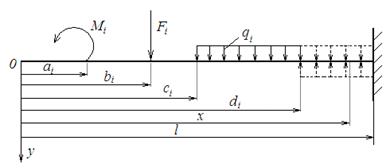
Рис.4.38

Рассмотрим консольную балку при плоском изгибе, на которую действуют все наиболее распространенные типы нагрузок: сосредоточенная сила F, сосредоточенный момент M и равномерно распределенная нагрузка с интенсивностью q (рис.4.38). Полагаем, что изгибная жесткость сечения балки по длине не изменяется (EI_z = const). Согласно принятым положениям, введем систему координат с началом на левом краю балки. Поскольку распределенная нагрузка заканчивается не на правом краю, продлеваем ее до края и вводим компенсирующую нагрузку (изображена штриховыми линиями).

Дифференциальное уравнение изогнутой оси балки в произвольном ее сечении х (при d < x < l) имеет вид

.

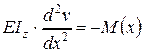Запишем в этом сечении изгибающий момент (по левым силам)

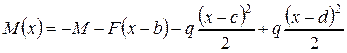
и подставим его в уравнение изогнутой оси балки

.

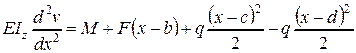Умножим полученное дифференциальное уравнение на dx и проинтегрируем его в пределах от 0 до х. В результате интегрирования получим:

1. Интеграл от левой части уравнения

.

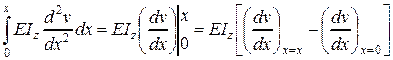Здесь: 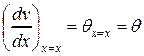- угол поворота сечения на расстоянии х от начала координат, т.е. угол поворота рассматриваемого произвольного сечения;

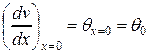- угол поворота сечения в начале координат, т.е. угол поворота крайнего левого сечения балки.

2. Интеграл от правой части уравнения

.

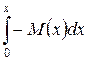Этот интеграл представляет собой площадь эпюры изгибающего момента, при определении которой используем принцип независимости действия сил, т.е. будем суммировать площади эпюр от каждого силового фактора в пределах действия этого фактора. В результате такого интегрирования будем иметь

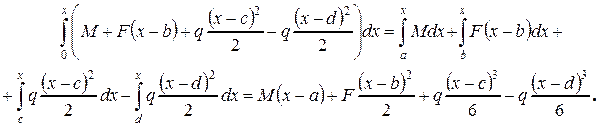
Приравняем результаты интегрирования правой и левой частей уравнения, разделим полученное соотношение на 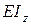и перенесем 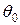в правую часть, получим

.

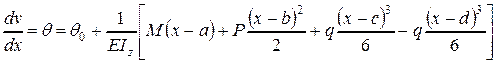Интегрируя аналогично, в тех же пределах, полученное выражение (заметим, что это можно делать без раскрытия скобок – интегрирование по А.Клебшу), в результате будем иметь

.

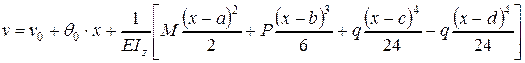Здесь: 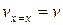- прогиб балки на расстоянии х от начала координат, т.е. прогиб балки в рассматриваемом произвольном сечении;

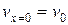- прогиб в начале координат, т.е. прогиб в крайнем левом сечении балки.

В случае действия нескольких (n) однотипных нагрузок, согласно принципу независимости действия сил, будем иметь

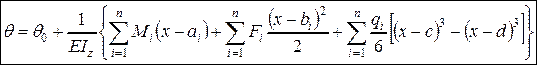, (4.19)

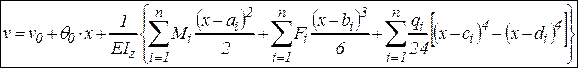(4.20)

Эти соотношения являются формулами метода начальных параметров для угла поворота произвольного сечения балки (4.19) и прогиба в этом сечении (4.20). Последнюю формулу называют также универсальным уравнением упругой линии балки.

Здесь: θ ₀, 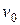- начальные параметры (угол поворота и прогиб в начале координат, т.е. на левом краю балки);

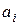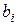, - расстояния от начала координат до сечений, в которых приложены соответственно сосредоточенные моменты 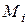и силы 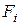(как активные, так и реактивные);

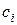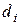, - расстояния от начала координат до начала и конца распределенной нагрузки.

Правило знаков:

- прогиб 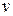– положителен, если направлен вниз;

- угол поворота сечения θ – положителен, если направлен по часовой стрелке;

- нагрузк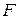и и 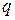– положительны, если направлены вниз;

- момент 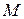– положителен, если направлен против движения часовой стрелки.

В формулы (4.19), (4.20) подставляются только те активные и реактивные нагрузки, которые расположены слева от сечения, где определяются угол поворота сечения и прогиб.

Начальные параметры θ ₀, и 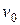, необходимые для проведения расчета по формулам (4.19), (4.20), определяются по этим же формулам из условий закрепления балок.