Теория по ТВ – часть 2

1. Случайной величиной называется функция, которая каждому элементарному исходу эксперимента ставит в соответствие некоторое число. Случайная величина обозначается .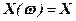

Если множество значений случайной величины дискретно, т. е. значения случайной величины отстоят друг от друга на числовой оси, то случайная величина называется дискретной.

Если множество значений случайной величины континуально, т.е. значения случайной величины полностью занимают некоторый промежуток числовой оси, то случайная величина называется непрерывной.

2. Закон распределения случайной величины – это соответствие между ее значениями и вероятностями, с которыми она принимает эти значения.

Закон распределения дискретной случайной величины представляется таблицей

…

…

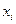
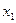
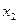
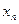
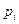
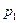
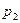
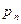
Здесь 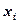- значения случайной величины Х; 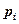= Р(Х = ).

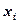Графическое представление закона распределения – многоугольник распределения. Это ломаная линия с узлами в точках .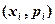

3. Функция распределения случайной величины Х находится по формуле: .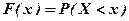

Основные свойства функции распределения:

1. .

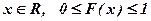2. 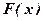– неубывающая функция.

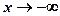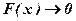3. при , ; при , .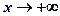

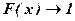4. .

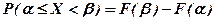Примерный вид графика функции распределения непрерывной случайной величины:

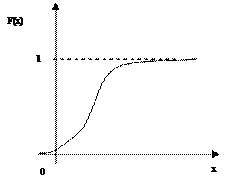
4. Плотность распределения вероятностей непрерывной случайной величины Х находится по формуле: .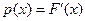

Основные свойства плотности распределения:

1. ,

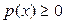2. 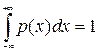– условие нормировки

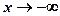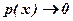3. при , ; при , .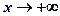

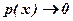4. .

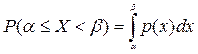5.

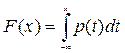
Примерный вид графика плотности распределения непрерывной случайной величины:

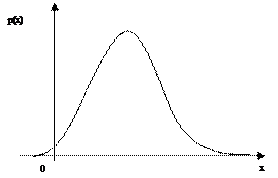
5. Математическое ожидание случайной величины Х – это ее среднеожидаемое значение. Математическое ожидание М(Х) можно назвать также серединой облака рассеивания значений случайной величины Х.

Для дискретной случайной величины М(Х) = 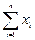. Для непрерывной случайной величины .

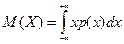Свойства математического ожидания:

М(С)=С, где С - const

М(СХ)=С М(Х)

М(Х+С)=М(Х)+С

М(Х+Y)=M(X)+M(Y)

M(XY)=M(X)M(Y), если Х и Y – независимые случайные величины.

6. Дисперсия случайной величины Х – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = .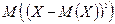

Дисперсия характеризует ширину разброса случайной величины вокруг ее математического ожидания.

Для дискретной случайной величины D(Х) = 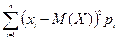. Для непрерывной случайной величины .

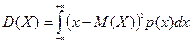Свойства дисперсии:

D(С)=0, где С - const

D(СХ)=С 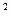D(Х)

D(Х+С)=D(Х)

D(Х+Y)=D(X)+D(Y), если Х и Y – независимые случайные величины

Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е. .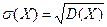

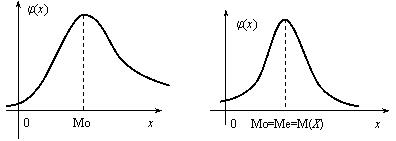
7. Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис. 1), а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис. 2).

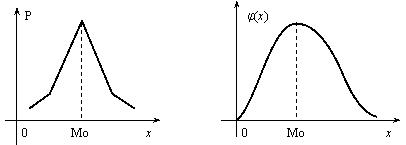
8. Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е. Р(Х < Ме) = Р(X > Ме). Из определения медианы следует, что Р(Х<Ме) = 0,5, т.е. F (Ме) = 0,5. Геометрически медиану можно истолковывать как абсциссу, в которой ордината φ(x) делит пополам площадь, ограниченную кривой распределения (рис. 1). В случае симметричного распределения медиана совпадает с модой и математическим ожиданием (рис. 2).

9. Начальным моментом k-го порядка ν_k случайной величины Х называется математическое ожидание величины Х^k, т.е. .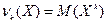

Начальный момент первого порядка – это математическое ожидание случайной величины.

Для дискретной случайной величины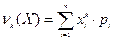

Для непрерывной случайной величины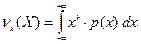

10. Центральным моментом k-го порядка μ_k случайной величины Х называется математическое ожидание величины (Х–М(Х))^k, т.е. .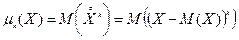

Центральный момент второго порядка – это дисперсия случайной величины.

Для дискретной случайной величины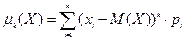

Для непрерывной случайной величины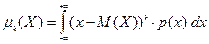

11. Величина 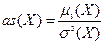называется коэффициентом асимметрии.

Свойства коэффициента асимметрии:

as(X)=0, распределение симметрично относительно М(Х).

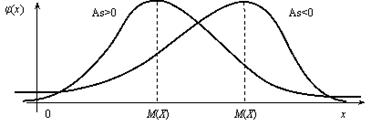
as(X)>0, распределение обладает правосторонней асимметрией.

as(X)<0, распределение обладает левосторонней асимметрией.

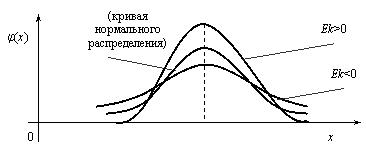
12. Эксцессом называется величина 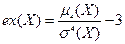. Эксцесс служит для сравнения соответствующего распределения с нормальным, у которого эксцесс равен нулю. Распределения более островершинные, чем нормальное, имеют эксцесс ех > 0, а более плосковершинные – имеют эксцесс ех < 0 (рис).

13. Типовые законы распределения: