Характеристическая постоянная передачи

Для определения характеристической постоянной передачи 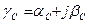рассматриваемых схем воспользуемся выраже­нием (10.57) и зависимостями между параметрами четырехпо­люсника (табл. 10.1), из которых найдем

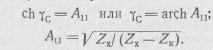
Подставив впоследнее выражение найденные выше сопротив­ления Z_xи Z_K, для обеих рассматриваемых схем получим одно и то же выражение . При этом будем иметь

При анализе фильтров вместо иногда удобнее пользовагься . Для этого воспользуемся известным изтригономет рии выражением

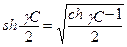
Учитывая (11.3), получим

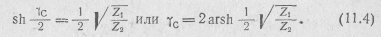
11.2.3. Полосы пропускания изадерживания

Полосой пропускания чисто реактивного фильтра называют интервал частот, впределах которого характеристическое затуха­ние α_с равно нулю, аполосой задерживания — интервал частот, где это затухание отлично от нуля. Иногда эти полосы называют характеристическими, чтобы отличить их от соответствующих по­лос, определение которых дано в начале раздела.

Учитывая, что ch jx= cos x, для полосы пропускания, впреде­лах которой α_с =0, будем иметь

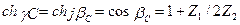
Имея в виду, что cos x может изменяться впределах ,получим

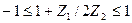или 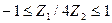. (11.5)

Это неравенство определяет условия полосы пропускания. Его иногда называют условием «прозрачности». Из этого неравенства следует, что вполосе пропускания сопротивления Z_l и Z ₂должны

быть чисто реактивными и противоположными по знаку (х_с или x_l), причем .

Условиями полосы задерживания являются:

τ. е. полоса задерживания будет в случае, если сопротивления плеч Z ₁и Z₂ имеют одинаковые знаки, или в случае если эти со­противления имеют разные знаки, но .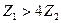

Полученные неравенства (11.5) и (11.6) можно использовать для нахождения полос пропускания и задерживания графическим методом. Для этого необходимо построить на одном графике ча­стотные зависимости сопротивлений Z ₁и 4Z₂.

Найдем выражения для расчета характеристических коэффи­циентов затухания и фазы в полосах пропускания и задерживания.

В полосе пропускания 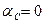и .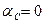

Подставив это значение yc в выражение (11.4), получим

В полосе задерживания .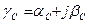

Подставив это выражение в формулу (11.4), получим

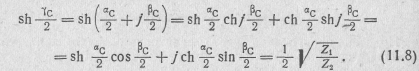
В большинстве случаев сопротивления Z ₁и Z₂ являются реак­тивными сопротивлениями противоположного знака. При этом

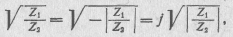
следовательно,

Отсюда видно, что в полосе задерживания должно выполняться равенство

Так как в рассматриваемой полосе 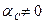, то из последнего ра­венства следует, что

откуда

. (11.10)

Подставив это значение в выражение (11.9), получим

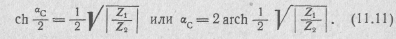
Таким образом, в полосе задерживания ßα является постоян­ной величиной, равной 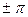, а определяется выражением (11.11).