Амплитудно-модулированные колебания

Для передачи информации в радиотехнике используются радио-волны — высокочастотные электромагнитные колебания, которые возможно эффективно излучать с помощью антенных устройств и которые способны распространяться в пространстве.

Передаваемая информация должна быть тем или иным спосо­бом заложена в высокочастотное (несущее) колебание. Это осу­ществляется с помощью модуляции. Модуляцией называется из­менение параметров несущего колебания по закону передаваемого сообщения. Модуляция, как правило, не оказывает влияния на способность высокочастотных колебаний распространяться в про­странстве.

В самом общем случае, модулированный сигнал можно предста­вить в виде колебания:

a (t)=A_m (t) cos [ωt+ψ (t)]=A_m (t) cos θ (t), (15.37)

в котором амплитуда А_т или фаза φ изменяется по закону пере­даваемого сообщения.

Если А_т и ψ — постоянные величины, то это выражение описы­вает простое гармоническое несущее колебание, не содержащее в себе никакой информации.

В зависимости от того, какой из двух параметров изменяется — амплитуда А_т или угол θ — различают два основных вида модуля­ции: амплитудную и угловую.

Угловая модуляция в свою очередь подразделяется на частот­ную и фазовую модуляции. Эти два вида модуляции между собой тесно связаны, различие между ними проявляется лишь вхарак-

тере изменения во времени угла θ при одном и том же законе мо­дуляции.

Для большинства используемых в радиотехнике сигналов ха­рактерно, что при модуляции параметры радиосигнала изменяются настолько медленно, что в пределах одного периода высокочастот­ного колебания его можно считать синусоидальным. Поэтому функции A_m(t), ψ(t), θ(t) можно считать медленно изменяющи­мися функциями времени.

Модулированные колебания в общем не являются периодиче­скими и относятся к числу квазигармонических, почти периоди­ческих функций. Такие функции могут быть разложены в триго­нометрический ряд и представлены как сумма гармонических со­ставляющих, частоты которых в общем случае не являются крат­ными, представляют комбинации частот и называются комбина­ционными. В отличие от такого ряда ряд Фурье содержит гармо­нические составляющие с кратными частотами.

В развитии теории модулированных колебаний большую роль сыграли работы Л. И. Мандельштама, П. Д. Папалекси, М. В. Шулейкина, В. И. Сифорова, И. С. Гоноровского и других советских ученых. В наиболее полном виде строгая математическая форму­лировка основных свойств модулированных колебаний и единых методов их исследования была впервые дана в монографии С. М. Рытова «Модулированные колебания и волны» (1940г.).

Амплитудная модуляция (AM) относится к числу простейших и получивших широкое применение благодаря своей простоте в осуществлении и использовании. При АМ амплитуда несущего колебания является функцией времени вида

A_m(t) = A_m0(l+F(t)], (15.38)

где A_m0 — постоянная, равная среднему значению амплитуды;

F(t) —функция времени, изменяющаяся по такому же закону, что и модулирующий сигнал, и называемая модуляцион­ной функцией.

Способы осуществления АМ обычно основаны на изменении по­тенциалов электронных приборов, входящих в состав радиопере­дающего устройства. В простейшем случае амплитудно-модулированное (АМ) колебание тока можно получить в цепи с изменяю­щимся сопротивлением, к которому приложено напряжение высо­кой частоты, а закон изменения определяется модуляционной функцией. Подобным переменным сопротивлением может служить, например, угольный микрофон.

Аналитически АМ колебания определяются выражением вида

α(t) = A_m0[1+ F (t)] cos(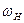 t + 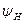). (15.39)

При гармонической (однотональной) модуляции, когда

F(t) = mcos (Ω t + φ₀), (15.40)

для АМ колебания получаем

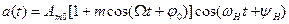, (15.41)

где т — коэффициент модуляции;

Ω — частота модуляции.

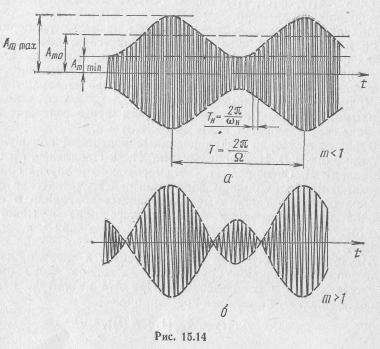
Коэффициент модуляции т пропорционален интенсивности пе­редаваемого сигнала, его называют также глубиной модуляции. При 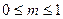амплитуда АМ колебания не принимает отрицатель­ных значений. Такая модуляция называется неискаженной (рис. 15.14, а). При m >1 значения A_m(t) на некоторых интерва­лах времени становятся отрицательными (рис. 15.14,6), что при­водит к перемодуляции, связанной с искажением огибающей коле­бания. Во избежание этого коэффициент модуляции выбирают не более единицы.

При неискаженной модуляции амплитуда АМ колебания из­меняется в пределах от А_{т min} = A_mo (1 - т) до A_mmax=A_mo (1 + m). При этом коэффициент модуляции может быть найден как отно­шение максимального приращения ΔA_т амплитуды колебаний к среднему ее значению A_m0:

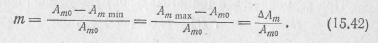
Следует заметить, что даже при модуляции простейшим гармо­ническим сигналом АМ колебание представляет собой сложный сигнал, состоящий из ряда гармонических составляющих. Эта особенность была установлена еще в 1913 г. московским профес­сором Н. Н. Андреевым, а затем подробно исследована в работах М. В. Шулейкина (1916 г.). Тем не менее в свое время (1930 г.) американским ученым Флемингом была поднята дискуссия о «ре­альности» дополнительных гармонических составляющих в АМ колебании с далеко идущими практическими выводами. Он утвер­ждал, что временное представление АМ колебания (15.39) отоб­ражает реальную ситуацию, а его спектральное представление является математической фикцией. По мнению Флеминга, в дей­ствительности никаких дополнительных частот нет, реальна лишь несущая частота, а следовательно, ширина спектра АМ колеба­ния бесконечно мала и точное воспроизведение сигнала возможно при сколь угодно малой полосе пропускания приемника, на­строенного точно на несущую частоту. Из этого делался вывод о возможности безграничного уплотнения эфира.

В настоящее время в справедливости спектрального представ­ления сомнений нет, а окончательный вывод Флеминга представ­ляется наивным. Для обычно используемых фильтров с постоян­ными параметрами гармонический спектр АМ сигнала не менее реален, чем его временное представление. Спектр можно наблю­дать и исследовать с помощью анализаторов спектра.

Как следует из формулы (15.41), при гармонической (одното­нальной) амплитудной модуляции

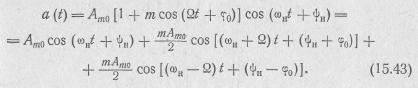
Первое слагаемое здесь представляет несущее колебание с ча­стотой ω_н. Второе и третье слагаемые соответствуют новым гар­моническим составляющим, появляющимся в процессе модуляции амплитуды. Они являются продуктом модуляции и называются боковыми гармоническими составляющими. Частоты этих колеба­ний (ω_н + Ω) и (ω_н —Ω) называются боковыми: верхней и нижней боковой частотой соответственно. Амплитуды этих составляющих одинаковы и зависят от глубины модуляции ( рис. 15.15,а), а их фазы симметричны относительно фазы несущего колебания. Чем меньше коэффициент т, тем меньше амплитуды боковых состав­ляющих, и в пределе при т =0 они отсутствуют.

Если модулирующий сигнал является сложнымз

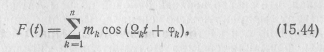
то каждая его гармоническая составляющая дает пару боковых частот:

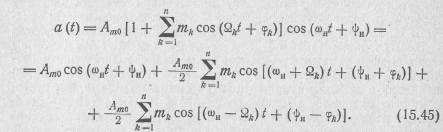
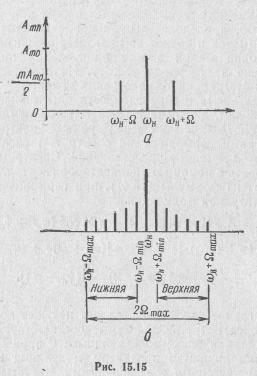
В результате получается спектр, состоящий из двух полос ча­стот, расположенных симметрично относительно несущей ча­стоты ω_н. Эти полосы частот, расположенные по обе стороны от несущей, называются боковыми: верхней и нижней боковой поло­сой (рис. 15.15,6).

Сравнивая спектры модулирующего сигнала (модулирующей функции) и соответствующего ему АМ колебания, можно сделать вывод, что спектр верхней боковой полосы AM колебания подобен спектру модулирующего сигнала. Разница лишь в том, что он сдвинут по оси частот на величину ω_н. При AM происходит лишь трансформация спектра модулирующего сигнала по оси частот.

Если полоса частот модулирующего сигнала ограничена сверху максимальной частотой йтах, то соответствующий ему AM сигнал будет иметь спектр (см. рис. 15.15,6), ширина которого вдвое больше:

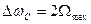(15.46)

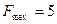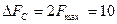Для телевизионных сигналов, например, МГци МГц.

При одновременной работе в данном диапазоне частот не­скольких радиопередающих устройств во избежание помех при приеме за счет перекрытия необходимо, чтобы несущие частоты ближайших (по шкале частот) станций были разнесены одна от другой не менее чем на .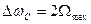

Довольно широкий диапазон частот, занимаемый АМ сигна­лами, является недостатком такого вида модуляции. К числу дру­гих серьезных недостатков АМ следует отнести плохую помехоза­щищенность и низкую экономичность радиопередатчиков. Указан­ные недостатки устраняются или в значительной мере снижаются при других видах модуляции, в частности при угловой модуляции.

Частным случаем АМ колебаний является последовательность когерентных прямоугольных радиоимпульсов (рис. 15.11). Такие колебания называют манипулированными. Различают соответ­ственно амплитудно-, фазо- и частотно-манипулированные сиг­налы.