Непериодических сигналов

Многие важные - сигналы не являются периодическими или почти периодическими и поэтому не могут быть представлены в виде ряда Фурье или тригонометрического ряда. К их числу в первую очередь следует отнести различные одиночные импульсы и совокупности конечного числа одиночных импульсов.

Чтобы применить спектральный метод для описания таких сигналов, предположим, что они являются периодическими функ­циями с периодом Т. Воспользовавшись при этом разложением в ряд Фурье и устремив 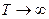. вернемся к исходной непериодиче­ской функции. Тогда и представление непериодических сигналов по Фурье может рассматриваться как предел ряда Фурье при .

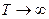В зависимости от того, из какой формы записи ряда Фурье исходить: вещественной (15.1) — (15.6) или комплексной (15.7), (15.8), будет получено спектральное представление непериодиче­ских сигналов в плоскости вещественных или комплексных вели­чин. В первом случае спектральные характеристики сигнала опре­деляются в области положительных частот от 0 до + 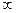, во вто­ром— в области как положительных, так и отрицательных частот, т. е. в пределах от — 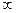до + .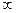

Наиболее удобной и компактной является комплексная форма записи, позволяющая часто значительно упростить расчеты. Под­ставим значения коэффициентов С _n из формулы (15.8) в выраже­ние ряда (15.7). Тогда, обозначив интервал между соседними частотами гармоник 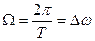, получим _ж

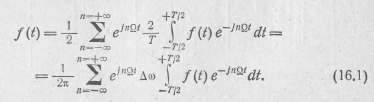
По мере возрастания Периода Т амплитуда гармоник С_п умень­шается, интервал Δω между соседними частотами в спектре со­кращается и линейный спектр все более сгущается. В пределе при 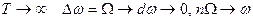, т. е. спектр из дискретного превращается в сплошной. При этом сумма в правой части (16.1) переходит в интеграл и получается выражение, называемое двойным интегралом или двойным преобразованием Фурье в ком­плексной форме:

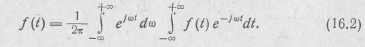
Эта формула Фурье имеет силу, если функция ƒ(t) абсолютно

интегрируема в пределах 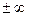, т. е. существует интеграл 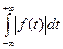кроме того, удовлетворяет условиям Дирихле во всяком конечном интервале. Однако условие абсолютной интегри­руемости не является необходимым, а только достаточным. Хотя этому условию удовлетворяют все реальные сигналы, существует ряд идеализированных сигналов, например ступенчатая l(t), си­нусоидальная sin ω₀t функции, не интегрируемые абсолютно, но представимые в виде интеграла Фурье.

Формула Фурье (16.2) представляет собой сумму бесконечно большого числа гармонических функций с бесконечно малыми амплитудами и с частотами ω, проходящими весь спектр от — оо до +.00. В самом деле, комплексное выражение

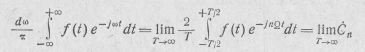
представляет собой бесконечно малую по модулю комплексную амплитуду гармоники частоты ω (конечный интеграл, умноженный на бесконечно малую величину d _ω).

Таким образом, приходим к выводу, что непериодические сиг­налы характеризуются непрерывным, сплошным спектром частот, в то время как периодические — дискретным или линейчатым спектром.

Формулу (16.2) можно переписать следующим образом:

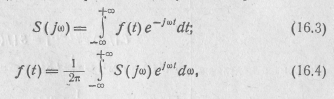
что представляет собой взаимно связанные интегральные уравне. ния, каждое из которых служит решением другого. Выражение (16.3) называется прямым преобразованием Фурье, а ( 16.4) —

обратным преобразованием Фурье, и они часто обозначаются со­ответственно как

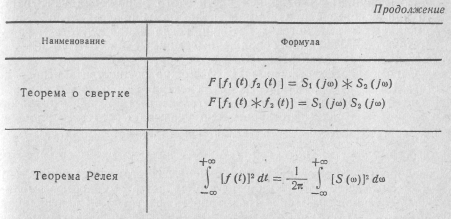
Прямое преобразование Фурье позволяет перейти от временной области представления функции на комплексную плоскость, а об­ратное преобразование, наоборот, — с комплексной плоскости на временную. Основные свойства преобразований Фурье приведены в табл. 16.1.

Величина S(jω) обычно называется спектральной плотностью, спектральной характеристикой или просто спектром непериодиче­ского сигнала. В общем случае

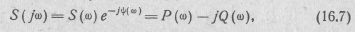
где S(ω) = |S(j ω)| —амплитудно-частотная характеристика или спектр;

ψ(ω) = argS(jω) —фазо-частотная характеристика или спектр;

P(ω)=ReS(jω) — вещественная частотная характеристика или спектр;

Q(ω) = JmS(jω) — мнимая частотная характеристика или спектр.

Спектральная плотность является комплексной функцией одной переменной — вещественной частоты ω. Поэтому ее компоненты: модуль, фазу, вещественную и мнимую составляющие — можно изобразить в виде графиков-спектров.

Отметим, что при использовании комплексной формы преобра­зований Фурье (16.2) — (16.4) указанные спектры захватывают всю область как положительных, так и отрицательных частот, так как согласно формуле (16.3) спектральная плотность, а следовательно, и все ее компоненты дают представление функции на комплексной плоскости.

Проводя аналогию между разложением в ряд Фурье и интегра­лом Фурье:

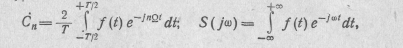
можно прийти к соотношению

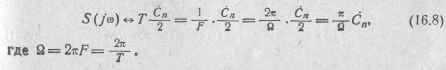
Коэффициент ¹/₂ в правой части этого выражения учитывает, что при использовании комплексной формы представления сину­соидальных гармонических величин, когда одной частоте ω соот­ветствуют две взаимно сопряженные мнимые частоты jω и —jω, амплитуды гармоник равны С_п/2.

С помощью соотношения (16.8) можно осуществить непосред­ственный переход, например, от спектра одиночного импульса к спектру периодической последовательности таких же импульсов и наоборот. С другой стороны, оно указывает, что спектральная плотность S ( eo) получается делением комплексной амплитуды C_n/2 n-й гармоники на интервал 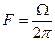, разделяющий по частоте соседние гармонические составляющие. Поэтому функция S(ω) имеет смысл плотности амплитуд и обладает размерностью ампли­туды, деленной на герц (размерность частоты). Спектральная плотность S(jω) характеризует по амплитуде и фазе гармонику частоты ω. Выражение 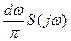является комплексной амплиту­дой этой гармоники, так как

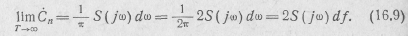
Из соотношения (16.8) вытекает также очень важный вывод: огибающая сплошного спектра S(ω) непериодической функции и огибающая линейчатого спектра периодической функции C_n(ω) совпадают по форме и отличаются лишь масштабом:

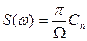
Если исходить из вещественной формы записи ряда Фурье (15.3), то, под­ставив в него значения коэффициентов (15.4) и обозначив Ω = Δω, получи м

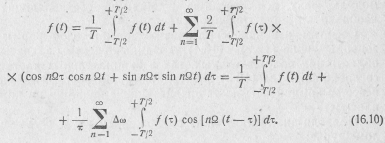
При 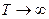здесь Δω превращается в dω, 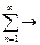в 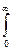. Тогда, считая функцию f(t) абсолютно интегрируемой в пределах ± 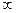и учитывая, что при этом первый интеграл в выражении (16.10) равен нулю, устремляя 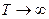, получим двойной интеграл или двойное преобразование Фурье в вещественной форме:

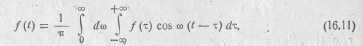
Эта формула Фурье Представляет собой сумму бесконечно большого числа гармонических функций — 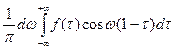с бесконечно малыми амплитудами и частотами, проходящими спектр от 0 до + 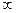. Ее можно предста­вить в ином виде. Преобразуя правую часть в выражении (16.11) и используя формулу для косинуса разности углов, найдем

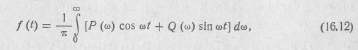
где

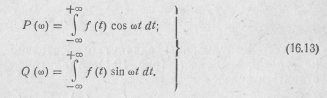
С другой стороны, обозначив

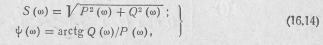
получим еще один вид интеграла Фурье в вещественной форме:

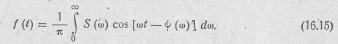
Полученные спектральные характеристики (16.13), (16.14) сигнала полностью совпадают с уже полученными выше (16.7). Однако при использовании веще­ственной формы интеграла Фурье они представляют функцию в плоскости ве­щественных величин и захватывают поэтому лишь область положительных частот от 0 до + .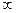

Сравнивая выражения (16.3) и (16.4), можно отметить суще­ственно симметричную природу прямого и обратного преобразова­ний Фурье. Это свойство основано на дуальности частоты и вре­мени.

Если в преобразованиях Фурье произвести взаимную замену переменных, а именно: заменить jω на t и t на jω, а затем заме

нить jω на -jω, то получим, что функция 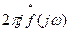будет спектром функции S(t), функция S(t)—обратным преобразованием функ­ции - :

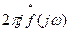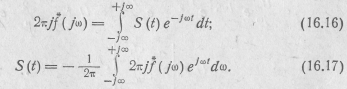
Иными словами, если спектром функции ƒ(t) является S(ω), то спектром функции S(t) будет .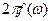

Указанное свойство частотно-временной двойственности, или дуальности, преобразований Фурье часто используется в теории сигналов. Оно позволяет взаимно менять местами временную функцию и ее спектр. Решению любой задачи из теории сигналов в частотной области соответствует решение дуальной ей задачи во временной области, и наоборот, хотя в конкретных случаях ре­шение дуальной задачи может и не иметь практического значения.