2015-05-13
7724
Рассмотрим одиночный прямоугольный радиоимпульс (рис. 16.3). Колебания подобного вида имеют большое практическое значение и широко применяются в радиолокации. Пусть
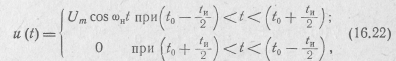
где ωн — частота несущего колебания.
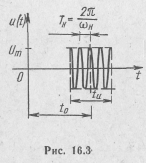Такой импульс можно рассматривать как произведение модуляционной функции вида прямоугольного одиночного видеоимпульса (16.18) и несущего косинусоидального колебания частоты ωн.
Зная спектральную плотность модуляционной функции (16.19) и используя свойство преобразования Фурье — свойство умножения функции времени на косинус (теорема о модуляции) (табл. 16.1):
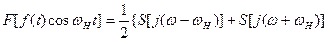
находим спектральную плотность радиоимпульса (см. рис. 16.3)
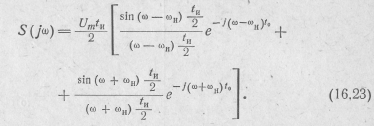
Она представляет спектральные характеристики сигнала на комплексной плоскости, т. е. в диапазоне частот от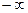 
до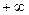 
.Исследуя полученное выражение в этом диапазоне, отметим, что модуль S(ω) имеет наибольшее значение в районе частот 
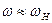, и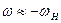 
. Объясняется это тем, что знаменатель одной из дробей в квадратной скобке делается в районе этих частот относительно малой величиной: при 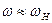вторая дробь значительно меньше первой, а при 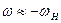, наоборот, первая дробь значительно меньше второй.
Таким образом, выражение (16.23) для спектральной плотности прямоугольного радиоимпульса в области положительных частот достаточно точно описывается первой дробью, а в области отрицательных частот — второй дробью. Поэтому можно приближенно записать:
для положительных частот:
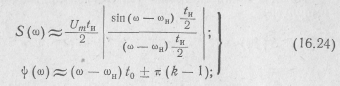
для отрицательных частот:
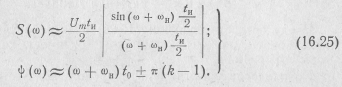
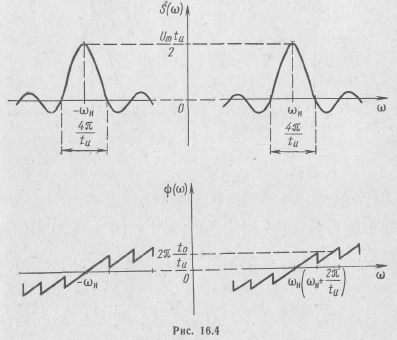
Спектры прямоугольного радиоимпульса представлены на рис. 16.4. Они практически отличаются от спектров прямоугольного видеоимпульса лишь смещением по оси частот на величину они уменьшением вдвое модуля спектральной функции.
