Для колоколообразного или «гауссова» импульса (рис. 16.5)
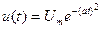 (16.26)
(16.26)
где α — постоянная, определяющая длительность импульса.
Па основании формулы (16.3) спектральная плотность такого импульса
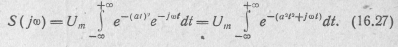
Для вычисления интеграла преобразуем показатель степени:
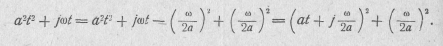
Произведя замену переменных 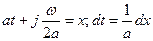 , пoлучим
, пoлучим
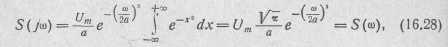
так как 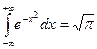 —интеграл Лапласа.
—интеграл Лапласа.
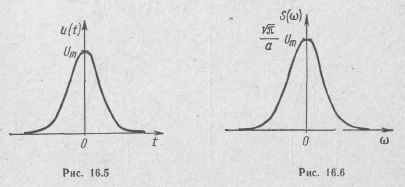
Ввиду четности функции (16.26) спектр получился вещественным, причем, как и сам импульс, он имеет колоколообразную форму (рис. 16.6).
Колоколообразный импульс широко используется в теории сигналов, поскольку он и его спектр выражаются одинаковыми функциями и обладают свойством симметрии: чтобы получить одну из этих функций по заданной другой, достаточно заменить t на ω. Исключительно большое практическое значение импульса колоколообразной формы объясняется минимальным значением произведения 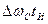 . Это значит, что по сравнению с импульсами другой формы колоколообразный импульс той же длительности имеет наименьшую ширину спектра и поэтому более помехоустойчив. При энергетическом способе определения
. Это значит, что по сравнению с импульсами другой формы колоколообразный импульс той же длительности имеет наименьшую ширину спектра и поэтому более помехоустойчив. При энергетическом способе определения 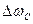 и
и 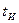 для колоколообразного импульса
для колоколообразного импульса 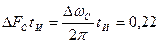 .
.
 2015-05-13
2015-05-13 4893
4893








