Основные положения и теоремы операционного исчисления

Для решения линейных дифференциальных и интегро-дифференциальных уравнений в теории электрических цепей нашел ши­рокое применение так называемый операторный метод, основан­ный на преобразованиях Лапласа.

Сущность этого метода заключается в том, что функции веще­ственного переменного t преобразуются в функции комплексного переменного ρ = σ+ƒω таким образом, чтобы вместо интегро-дифференциальных уравнений получить алгебраические уравнения. После решения этих уравнений производят обратный переход к функции вещественного переменного t. Это значительно упро­щает решение интегро-дифференциальных уравнений.

Переход от функции вещественного переменного t к функциям комплексного переменного р осуществляется с помощью прямого преобразования Лапласа:

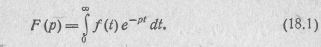
Обратный переход от функций комплексного переменного ρ к функциям вещественного переменного t осуществляют на осно­вании обратного преобразования Лапласа:

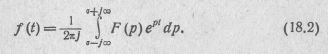
Функцию ƒ(t) называют оригиналом, а функцию F(p) —изо­бражением оригинала по Лапласу или просто изображением.

Напомним, что для того, чтобы функция ƒ(/) имела изображе­ние (18.1), необходимо, чтобы она:

а) удовлетворяла условиям Дирихле;

б) была равна нулю для отрицательных значений t, т. е. при t<0 ƒ(t)+0;

в) в интервале t от 0 до 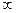не возрастала быстрее, чем неко­торая показательная функция

,

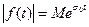где М и 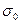— произвольные положительные числа, т. е. здесь не требуется абсолютная интегрируемость функции ƒ(t), как это тре­буется в интегралах Фурье. Поэтому преобразования Лапласа возможны для более широкого класса функций, чем преобразова­ния Фурье.

Напомним некоторые свойства преобразования Лапласа, из­вестные из математики.

1. Свойство линейности. Если 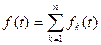, то

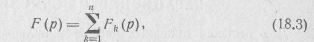
т. е. изображение суммы функций равно сумме изображений каж­дой из функций в отдельности.

2. Дифференцирование оригинала. Если 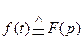, то

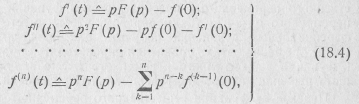
где ƒ^{(k- 1)}(0) —значение производной (k —1)-го порядка функции ƒ ( t) при t=0.

При нулевых начальных условиях, когда ƒ(0)=ƒ'(0) ==...= ƒ ^(n-1)=0,

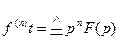, (18.5)

т. е. n-кратному дифференцированию оригинала соответствует п-кратное умножение изображения на оператор р.

3. Интегрирование оригинала. Если f(t) 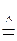F(p), то

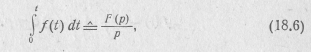
т. е. операции интегрирования оригинала в пределах от 0 до t со­ответствует деление его изображения на оператор р.

4. Теорема запаздывания. Если 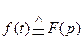, то

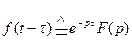, (18.7)

т. е. запаздыванию оригинала на время τ соответствует умноже­ние изображения на .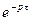

5. Теорема смещения. Если 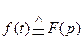, то

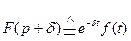, (18.8)

т. е. замене в изображении оператора р на оператор р + δ соответствует умножение оригинала на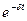

6. Умножение изображений (теорема свертывания). Если

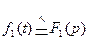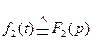и , то

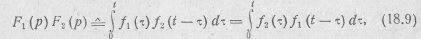
т. е. умножений изображении соответствует «свертывание» ориги­налов

Следствие: применяя правило дифференцирования ориги­нала к (18.9), получим

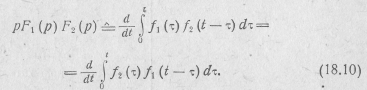
Это две формы записи интеграла Дюамеля, из которых можно получить остальные формы этого интеграла, рассмотренные в

разд. 14.

7. Теорема разложения. Если изображение имеет вид рацио­нальной дроби

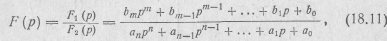
причем степень многочлена F₁(p) ниже степени многочлена F₂(р), коэффициенты a_k и b_k — вещественные числа, а корни р _kуравне­ния F₂(р) =0 различны, то оригинал определяется выражением

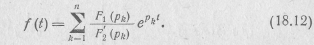
В случае если один из корней уравнения F₂(p)=Q равен нулю, т. е. F₂(p) = pF₃(p), то оригинал находится по формуле

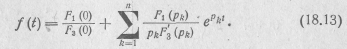
В случае если уравнение F ₂(p)=0 имеет кратные корни, то оригинал находится по формуле

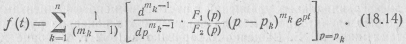
Теорема разложения в сочетании с другими свойствами пре­образования Лапласа дает возможность составить таблицы изо­бражений и оригиналов, облегчающие и ускоряющие нахождение оригиналов по изображениям [26]. Некоторые наиболее часто встречающиеся операторные соответствия приведены в табл. 18.1

Следует отметить, что возможность интегрирования линейных дифференциальных уравнений с постоянными коэффициентами с по­мощью операторного метода впервые была показана русским ма­тематиком М. Е. Ващенко-Захарченко в 1862 г, В конце XIX в.

английский ученый О. Хевисайд применил этот метод к расчету электромагнитных переходных процессов. Большой вклад в раз­витие операционного исчисления и его применение к расчету элек­тромагнитных процессов внесли советские ученые В. С. Игнатовский, А. М. Данилевский, А. М. Эфрос, К. А. Круг, М. И. Канторо­вич и др.