Приток упругой жидкости к скважине с постоянным расходом

В момент времени t = 0 в горизонтальном пласте постоянной толщины h пущена в эксплуатацию скважина радиусом r_c с постоянным дебитом Q_o. До пуска скважины давление во всем пласте было одинаковым и равным p_k. Обозначим длину зоны возмущение на момент времени t через R(t). Требуется найти закон перемещения во времени внешней границы возмущенной области.

Запишем формулу стационарнргостационарного распределения давления, вокруг скважины работающей с постоянным расходом и контуром питания равным длине возмущеннийвозмущенной области:

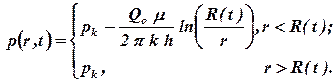(1.73)

Запишем уравнение материального баланса для скважины. Для этого проинтегрируем уравнение упруговоупругого режима по области фильтрации, то есть по площади от радиуса скважины до бесконечности:

.

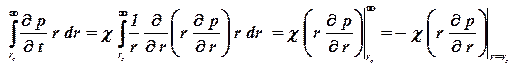(1.74)

Правая часть этого уравнения легко интегрируется. Так, как в невозмущенной области давление не меняется, то интеграл в левой части по невозмущенной области обращается в ноль, тогда уравнение материального баланса запишется

.

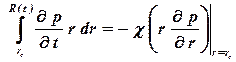(1.75)

Вычислим значения производных по времени и координате в возмущенной области и подставим их в уравнение материального баланса

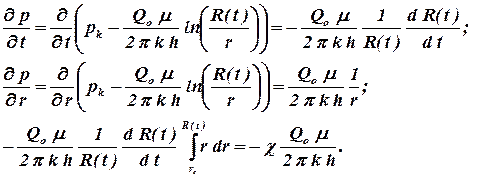(1.76)

В последнем уравнении интеграл легко вычисляется. Упростив уравнение получим

.

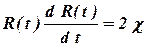(1.77)

Последнее уравнение легко интегрируется с условием, что в начальный момент времени длина возмущенной зоны равна радиусу скважины:

.

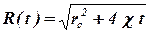(1.78)

Расход в любой точке пласта можно найти по закону Дарси. ВВ невозмущенной области давление не меняется, поэтому скорость фильтрации и дебит равен нулю. Внутри возмущенной области

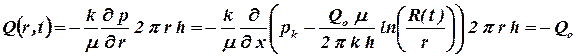(1.79)

Знак (-) означает, что вектор скорости фильтрации направлен против оси x. Будем считать дебит галереи положительным. Тогда расчет давлений и расходов по МПССС производится по формулам

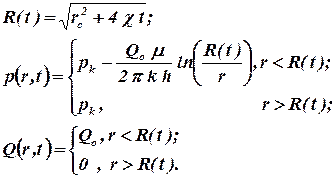(1.80)

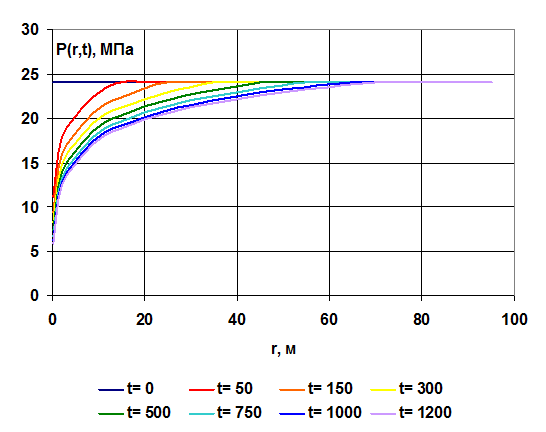Рис. 1.15. Распределение давления вокруг скважины, работающей с постоянным расходом по методу ПССС