Упругие волны в газах. Волновое уравнение

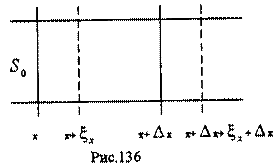
Для вывода волнового уравнения для газов выделим цилиндрический столб газа сечения S ₀, и длины Δx (рис.136). При распространении в столбе продольной звуковой волны граничные сечения испытывают смещения от первоначального положения. Смещение левого сечения равно ξ_x, а правого - ξ_x+Δx.

Удлинение столба равно разности смещений:

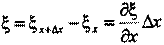Относительную деформацию объема, выделенного столба газа через удлинение постоянном сечении запишем в виде:

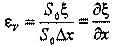Процесс распространения волны протекает настолько быстро, что теплообменом с окружающей средой можно пренебречь, т.е. процесс изменения состояния газа в выделенном столбе можно считать адиабатическим. Адиабатические процессы подчиняются уравнению р-V^γ = С, откуда: dpV^γ + γ V^γ-1∙pdV=0. Учитывая это, установим связь между относительной деформацией объёма и относительным изменением давления:

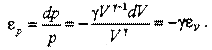На торцы столба газа действуют силы давления. Если давление на левом торце равно

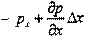
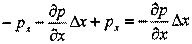p_x,то на другом торце. Разность сил давления, действующих на столб газа в направлении распространения волны, равна:.

Масса газа может быть выражена соотношением ρ₀S₀Δx, где ρ₀ - плотность в недеформированном столбе длины Δх. По второму закону Ньютона

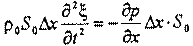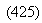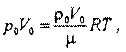Плотность газа ρ₀ можно получить из уравнение состояния газа для начального (недеформированного) состояния:

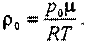откуда:

Подставив выражение плотности в уравнение движения, получим:

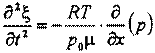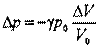Давление р определяется через начальное давление и его изменение Δр при деформации столба: р=р₀+Δр. Используя связь между относительным изменением давления и относительной деформацией объема, полученную ранее, изменение давления запишется в виде:

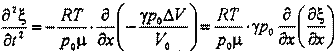С учетом сказанного уравнение движения. для выделенного столба газа представим в виде:

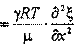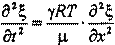т.е.

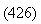Это и есть волновое уравнение для газа. Решением волнового уравнения является уравнение плоской волны:

ξ = a sin(ωt - kx)

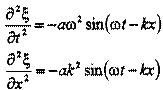Учитывая, что:

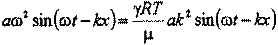получаем после подстановки этих значений в волновое уравнение:

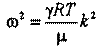Очевидно, что равенство выполняется при условии, что:

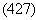
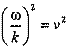Так как, скорость волны в газе равна:

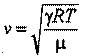Скорость волны в газах, как видим, не зависит от давления, а определяется родом газа (значениями γ и μ) и его температурой Т.

Если рассмотреть подобным образом распространение волны в произвольном направлении в пространстве, уравнение волны получим в виде:

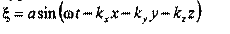где: k_x,k_y,k_z - проекции волнового вектора на оси координат.