С увеличением порядка дифференциальных уравнений САУ более трудно анализировать качество переходного процесса. Для этого случая в ТАУ введены интегральные оценки при использовании которых можно выбирать параметры САУ соответствующие минимальному времени переходного процесса.
Как уже известно, переходный процесс был бы идеальный, если бы в момент возникновения управляющего воздействия регулируемый параметр принимал бы мгновенно новое установившееся значение и не изменялся бы до возникновения нового воздействия. В реальном процессе это невозможно. Отличие реального процесса от идеального тем больше, чем больше площадь, заключенная между кривыми этих процессов (рис. 5.6,а). Степень отличия реального и идеального переходного процессов оценивается интегральными оценками.
Простейшей интегральной оценкой является
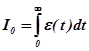 ,
,
где 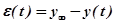 - отклонение регулируемого параметра от нового установившегося значения. Геометрически
- отклонение регулируемого параметра от нового установившегося значения. Геометрически 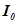 выражает площадь под кривой переходного процесса, построенного по отклонению. Заштрихованная площадь будет тем меньше, чем меньше величина отклонения
выражает площадь под кривой переходного процесса, построенного по отклонению. Заштрихованная площадь будет тем меньше, чем меньше величина отклонения 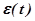 и быстрее затухает переходный процесс. Следовательно, чем меньше
и быстрее затухает переходный процесс. Следовательно, чем меньше 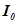 , тем лучше переходный процесс в САУ. Рассмотрим выбор параметров САУ на основе интегральной оценки
, тем лучше переходный процесс в САУ. Рассмотрим выбор параметров САУ на основе интегральной оценки 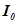 .
.
 2015-05-13
2015-05-13 553
553








