Характеристического уравнения

Метод определения параметров САУ по распределению корней характеристического уравнения в основном применяется для систем с передаточной функцией вида

.

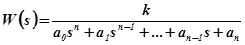Корни характеристического уравнения данной системы, распределенные определенным образом на левой полуплоскости корней, полностью определяют качество переходного процесса в системе. 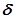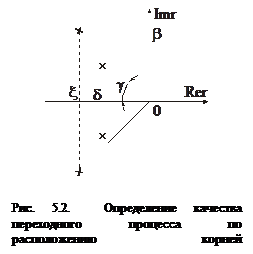Так как трудно анализировать влияние каждого корня на качество переходного процесса и на основе этого выбирать параметры системы управления, вводят косвенные оценки распределения корней характеристического уравнения: степень устойчивости и колебательность 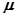(рис. 5.2).

Для определения параметров САУ с использованием этого метода сначала необходимо выяснить с одной стороны связь этих оценок с распределением корней характеристического уравнения на комплексной плоскости корней, а следовательно, и с параметрами системы, а с другой стороны – связь этих оценок с показателями качества переходного процесса.

Степень устойчивости 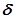САУ представляет собой модуль вещественной части корня, наиболее близко расположенного к мнимой оси комплексной плоскости корней 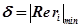. Величина 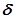характеризует длительность переходного процесса. Корни с наименьшей по абсолютной величине вещественной частью дают в переходном процессе составляющие, которые затухают медленнее других.

Оценивая приближенно длительность переходного процесса только по ближайшему к мнимой оси корню, получим:

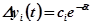- в случае вещественного корня и

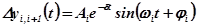(5.1)

- в случае комплексно-сопряженных корней.

Если за время регулирования 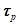составляющая 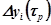(в случае вещественного корня) примет значение 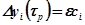, то длительность процесса определится из равенства 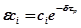и будет равна

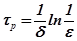, (5.2)

где 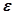- величина, показывающая во сколько раз уменьшается выходная величина за время регулирования.

К аналогичному соотношению можно прийти, рассматривая 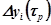для случая комплексных корней.

Колебательность системы управления 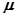определяется как тангенс угла, образованного осью абсцисс и прямой, проведенной из начала координат к точке, соответствующей корню, при проведении прямой через который, этим углом охватываются все корни в одной из четвертей левой полуплоскости корней, то есть 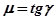(см. рис. 5.2).

Колебательность 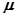характеризует перерегулирование и скорость затухания колебаний во время переходного процесса в системе. Действительно, наличие среди корней характеристического уравнения комплексно-сопряженных корней предопределяет колебательный характер переходного процесса, причем колебательная составляющая затухает по закону (5.1).

Определим затухание амплитуды колебаний за один период 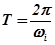. В некоторый момент времени 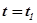эта амплитуда равна 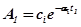, а через один период - 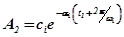. Затухание амплитуды колебаний за период равно

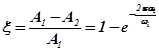
или

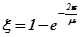(5.3)

Обычно затухание выражают в процентах . Из равенства (5.3), задавшись степенью затухания 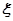можно определить колебательность

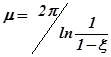. (5.4)

В САУ требуемое затухание колебаний за период составляет (90...98)%. Например, если 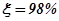, то допустимая колебательность 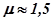, а при 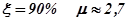. Таким образом, чем меньше затухание 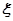, тем больше колебательность .

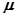Задавая значение 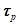и 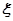, можно определить по формулам (5.2) и (5.4) косвенные оценк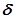и и 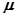качества переходного процесса в САУ. Для определения параметров системы необходимо связать их с 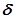и 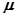. Для этого разработаны специальные методы, с использованием которых по заданному собственному оператору 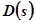системы находятся уравнения связ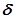и и 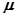с коэффициентами 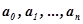, т. е. фактически с физическими параметрами САУ. Достаточно точные результаты получаются для систем с уравнением невысокого порядка. Например, И.А. Вышнеградским составлены такие уравнения для системы третьего порядка (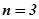) и построены номограммы в плоскости безразмерных комплексов А и В для сери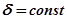й и 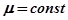. Так как при построении диаграммы И.А. Вышнеградского исходное уравнение приводилось к безразмерной форме (см. раздел 4), то относительная степень устойчивости равна

,

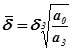а колебательность – величина безразмерная, т. е. .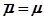

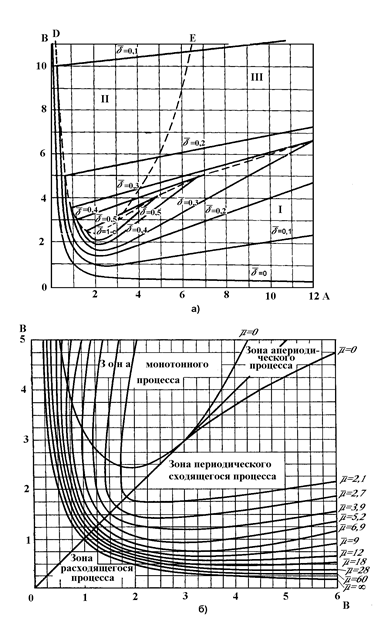
Рис. 5.3. Линии равных значений степени устойчивости (а) и колебательности (б) на диаграмме И.А. Вышнеградского.

Порядок выбора параметров САУ при заданных 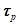и 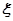таков, что по формулам (5.2) и (5.4) определяют 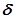и 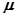. Задаваясь рядом коэффициентов, входящих в 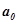и 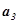, определяют 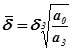и 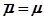. Из диаграммы И.А. Вышнеградского находят два безразмерных комплекса А и В,соответствующих пересечению кривых равной степени устойчивости 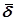и колебательности 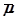. При этом целесообразно вначале провести анализ возможных вариантов переходного процесса в соответствии с рис. 5.3 и задать желаемый его характер изменения во времени. При известных величинах А и В, задаваясь всеми параметрами кроме двух, определяют искомые их величины из решения системы уравнений

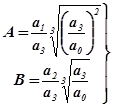
После того, как определены параметры всех звеньев регулятора, делают контрольный расчет характеристики САУ и сравнивают требуемые показатели качества переходного процесса с полученными в результате расчета. При удовлетворительном их совпадении приступают к конструированию регулятора, а при несовпадении повторяют вновь расчет параметров регулятора.