Определение 6

План 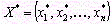, при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (8) при плане Х будем обозначать через 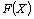. Следовательно, X^* – оптимальный план задачи, если для любого Х выполняется неравенство 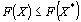[соответственно ].

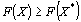Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти минимум функции 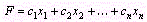, можно перейти к нахождению максимума функции 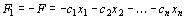, поскольку .

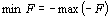Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “ 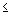”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “ 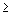” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

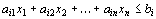
преобразуется в ограничение-равенство

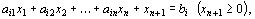(12)

а ограничение-неравенство

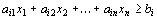
– в ограничение-равенство

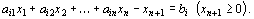(13)

В то же время каждое уравнение системы ограничений

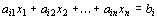
можно записать в виде неравенств:

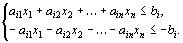(14)

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Отметим, наконец, что если переменная 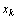, не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменным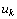и и 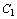, приняв .

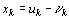Задача оптимального производственного планирования Для изготовления n видов продукции P1,…,Pn используется m видов сырья S1,…,Sm, запасы которого ограничены и составляют соответственно b1,…,bm единиц. Известно, что на производство единицы продукции Pj (j=) расходуется аij единиц ресурса Si (i=, а прибыль от реализации единицы продукции Pj (j= составляет сj (j=. Требуется определить план производства, который позволяет при наличных ресурсах получить максимальную прибыль предприятия от реализации продукции. Прежде всего запишем условия задачи компактно в виде таблицы: Вид продукции Вид сырья Р1... Pj... Pn Запас ресурса S1 a11... a1j... a1n b1..................... Si ai1... aij... ain bi..................... Sm am1... amj... amn bm Прибыль c1 … cj … cn Составим математическую модель задачи. Обозначим через xj (j=планируемое к выпуску количество продукции Рj (j=, а через Z (х1,…, xn) – прибыль предприятия от реализации всей продукции. Тогда планом производства будет вектор Х = (х1,…,хn), показывающий, какое количество продукции каждого вида будет произведено. Переменные х1,…,хn – управляемые переменные. Цель решения задачи (критерий оптимальности) – максимизировать прибыль: Z = c1x1 + c2x2 +... + cnxn. Суммарные затраты ресурса Si (i=составляют:. В силу ограниченности ресурса Si величиной bi получим систему ограничений:. На переменные хj должно быть наложено условие неотрицательности т.е. продукция Рj может либо выпускаться (xj > 0), либо не выпускаться (xj = 0). Итак, математическая модель примет вид:,.

43. 2.2 Алгоритм решения ЗЛП симплексным методом

Симплекс-метод подразумевает последовательный перебор всех вершин области допустимых значений с целью нахождения той вершины, где функция принимает экстремальное значение. На первом этапе находится какое-нибудь решение, которое улучшается на каждом последующем шаге. Такое решение называется базисным.

Первый шаг.В составленной таблице сначала необходимо просмотреть столбец со свободными членами. Если в нем имеются отрицательные элементы, то необходимо осуществить переход ко второму шагу, если же нет, то к пятому.

Второй шаг.На втором шаге необходимо определиться, какую переменную исключить из базиса, а какую включить, для того, что бы произвести перерасчет симплекс-таблицы. Для этого просматриваем столбец со свободными членами и находим в нем отрицательный элемент. Строка с отрицательным элементом будет называться ведущей. В ней находим максимальный по модулю отрицательный элемент, соответствующий ему

столбец - ведомый. Если же среди свободных членов есть отрицательные значения, а в соответствующей строке нет, то такая таблица не будет иметь решений. Переменная в ведущей строке, находящаяся в столбце свободных членов исключается из базиса, а переменная, соответствующая ведущему столбцу включается в базис. В Таб.2.1 приведен пример симплекс-таблицы.
Таблица 2.1 –Пример симплекс-таблицы

базисные переменные	Свободные члены в ограничениях	Небазисные переменные
x1	x2	...	xl	...	xn
xn+1	b1	a11	a12	...	a1l	...	a1n
xn+2	b2	a21	a22	...	a2l	...	a2n
…	…	...	...	...	...	...	...
…	…	…	…	…	…	…	…
…	...	...	...	...	...	...	...
xn+r	b2	ar1	ar2	...	arl	...	arn
…	…	…	…	…	…	…	…
…	...	...	...	...	...	...	...
…	…	…	…	…	…	…	…
xn+m	bm	am1	am2	...	aml	...	amn
F(x)max	F0	-c1	-c2	...	-c1	...	-cn

Третий шаг. На третьем шаге пересчитываем всю симплекс-таблицу по специальным формулам.

Четвертый шаг.Если после перерасчета в столбце свободных членов остались отрицательные элементы, то переходим к первому шагу, если таких нет, то к пятому.

Пятый шаг.Если Вы дошли до пятого шага, значит нашли решение, которое допустимо. Однако, это не значит, что оно оптимально. Оптимальным оно будет только в том случае, если положительны все элементы в F-строке. Если же это не так, то необходимо улучшить решение, для чего находим для следующего перерасчета ведущие строку и столбец по следующему алгоритму. Первоначально, находим минимальное отрицательное число в строке F, исключая значение функции. Столбец с этим числом и будем ведущим. Для того, что бы найти ведущую строку, находим отношение соответствующего свободного члена и элемента из ведущего столбца, при условии, что они положительны. Минимальное отношение позволит определить ведущую строку. Вновь пересчитываем таблицу по формулам, т.е. переходим к шагу 3.

Шестой шаг.Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена сверху и Fmax->?. Если в строке F и в столбце свободных членов все элементы положительные, то найдено оптимальное решение.
2.3 Решение задачи линейного программирования симплекс-методом
Идея симплекс-метода относительно проста. Пусть в задаче линейного программирования имеется п переменных и т независимых линейных ограничений, заданных в форме уравнений. Мы знаем, что оптимальное решение (если оно существует) достигается в одной из опорных точек (вершин ОДР), где по крайней мере k = n - m из переменных равны нулю.

Выберем какие-то к переменных в качестве свободных и выразим через них остальные т базисных переменных. Пусть, например, в качестве свободных выбраны первые k = n - m переменныхx1, x2,…,xk,а

остальные m выражены через них(формула 2.1):
xk+1=?k+1.1x1+?k+1.2x2+ +?k+1.kxk+?k+1;

xk+2=?k+2.1x1+?k+2.2x2+ +?k+2.kxk+?k+2;(2.1)

……………………………………

xn=?n1x1+?n2x2+ +?nkxk+?n.

Предположим, что все свободные переменныеx1, x2,…,xkравны нулю.

При этом мы получим:

xk+1=?k+1;

xk+2=?k+2;

…….. (2.2)

Xn=?n

Это решение может быть допустимым или недопустимым. Оно допустимо, если все свободные члены?k+1,?k+2,…,?n(2.2)неотрицательны. Предположим, что это условие выполнено. Тогда мы получили опорное решение. Но является ли оно оптимальным? Чтобы проверить это, выразим целевую функцию Z через свободные переменныеx1, x2,…,xk.
Z=?0+?1x1+?2x2+…+?kxk (2.3)
Очевидно, что приx1=x2=…=xk=0, Z=?0. Проверим, может ли быть улучшено решение, т. е. получено уменьшение функции Z c увеличением каких-нибудь из переменныхx1, x2,…, xk(2.2) (уменьшать их мы не можем, так как все они равны нулю, а отрицательные значения переменных недопустимы). Если все коэффициенты?1,?2,…,?kв (2.3) положительны, то увеличение каких-либо из переменныхx1,x2,…,xk(2.2) не может уменьшить Z; следовательно, найденное опорное решение является оптимальным. Если же

среди коэффициентов?1,?2,…,?kесть отрицательные, то, увеличивая некоторые из переменныхx1,x2,…,xk(те, коэффициенты при которых отрицательны), мы можем улучшить решение.

Пусть, например, коэффициент?1в (2.3) отрицателен. Значит, есть смысл увеличитьx1, т. е. перейти от данного опорного решения к другому, где переменнаяx1не равна нулю, а вместо нее равна нулю какая-то другая. Однако увеличиватьx1следует с осторожностью, так чтобы не стали отрицательными другие переменныеxk+1, xk+2,…,xnвыраженные через свободные переменные, в частности черезx1формулами (2.2).

Например, если коэффициент приx1в соответствующемxjуравнении (2.2) отрицателен, то увеличениеx1может сделатьxjотрицательным. Наоборот, если среди уравнений (2.2) нет уравнения с отрицательным коэффициентом приx1то величинуx1можно увеличивать беспредельно, а, значит, линейная функция Z не ограничена снизу и оптимального решения ОЗ не существует.

Допустим, что это не так и что среди уравнений (2.2) есть такие, в которых коэффициент приx1отрицателен. Для переменных, стоящих в левых частях этих уравнений, увеличениеx1опасно — оно может сделать их отрицательными.

Возьмем одну из таких переменныхxlи посмотрим, до какой степени можно увеличитьx1, пока переменнаяxlне станет отрицательной. Выпишемl-eуравнение из системы (2.2):
xl=?l1x1+?l2x2+…+?lkxk+?l (2.4)
Здесь свободный член?l?0, а коэффициент?l1отрицателен.

Легко понять, что если мы оставимx2=x3=…=xk=0, тоxkможно увеличивать только до значения, равного–?l/?l1,а при дальнейшем увеличенииx1переменнаяx1станет отрицательной.

Выберем ту из переменныхxk+1,xk+2,…,xn, которая раньше всех обратится в нуль при увеличении x1, т. е. ту, для которой величина–?l/?l1

наименьшая. Пусть это будетxr. Тогда имеет смысл разрешить систему уравнений (2.2) относительно других базисных переменных, исключаяиз числа свободных переменныхx1и переводя вместо нее в группу свободных переменныхxr. Действительно, мы хотим перейти от опорного решения, задаваемого равенствамиx1=x2=…=xn=0 к опорному решению, в котором ужеx1?0, аx2=…=xk=xr=0. Первое опорное решение мы получили, положив равными нулю все прежние свободные переменныеx1,x2,…,xkвторое мы получим, если обратим в нуль все новые свободные переменныеx2,x3,…,xk,xr.

Базисными переменными при этом будутxl,xk+1,xk+2,…,xr-1, xr-1,…,xr.

Предположим, что уравнения типа (2.2) для нового набора базисных и свободных переменных составлены. Тогда можно выразить через новые свободные переменные и линейную функцию Z.Если все коэффициенты при переменных в этой формуле положительны, то мы нашли оптимальное решение: оно получится, если все свободные переменные положить равными нулю. Если среди коэффициентов при переменных есть отрицательные, то процедура улучшения решения продолжается: система вновь разрешается относительно других базисных переменных, и так далее, пока не будет найдено оптимальное решение, обращающее функцию Z в минимум.

Пример 2. Пусть имеется задача линейного программирования с ограничениями-неравенствами:
-5x1-x2+2x3?2;

-x1+x3+x4?5; (2.5)

-3x1+5x4?7.
Требуется минимизировать линейную функцию
Z=5x1-2x3

Приводя неравенства к стандартному виду (?0) и вводя добавочные переменныеy1,y2,y3переходим к условиям-равенствам:

y1=5x1+x2-2x3+2

y2=x1-x3-x4+5 (2.5)

y3=3x1-5x4+7
Число переменных (n = 7) на 4 превышает число уравнений (т = 3). Значит, четыре переменные могут быть выбраны в качестве свободных.

Пусть в качестве свободных переменных выступаютx1,x2,x3,x4. Положим их равными нулю и получим опорное решение:
x1=x2=x3=x4=0;

y1=2, y2=5, y3=7.
При этих значениях переменных Z= 0.

Это решение не оптимально, поскольку в линейной функции Z коэффициент приx3отрицателен. Значит, увеличиваяx3можно уменьшить Z.

Попробуем увеличиватьx3.Из выражений (2.5) видно, что вy1и y2переменнаяx3входит с отрицательным коэффициентом, значит, при увеличенииx3соответствующие переменные могут стать отрицательными.

Определим, какая из этих переменных (y1илиy2)раньше обратится в нуль при увеличенииx3Очевидно, что этоy1она станет равной нулю приx3=1, а величинаy2— только приx3= 5.

Выбирается переменная у, и вводится в число свободных вместоx3Чтобы разрешить систему (2.5) относительноx3, y2, y3поступим следующим образом. Разрешим первое уравнение (2.5) относительно новой базисной переменнойx3:
x3=5/2*x1+1/2*x2-1/2*y1+1

Это выражение подставляется вместоx3во второе уравнение:

x3=5/2*x1+1/2*x2-1/2y1+1;

y2=-3/2*x1-1/2*x2+1/2*y1-x4+4; (2.6)

y3=3x1-5x4+7.
Что касается третьего уравнения, то оно, как не содержащееx3не изменится. Система (2.2) приведена к виду со свободными переменнымиx1, x2, y1, x4и базиснымиx3, y2, y3.

Положим теперь свободные переменные равными нулю. Функция приобретает значение Z=-2, что меньше (лучше), чем прежнее значение Z= 0.

Это решение все еще не оптимально, так как коэффициент приx2в выражении (2.7) отрицателен, и переменнаяx2может быть увеличена. Это увеличение, как это видно из системы (2.6), может сделать отрицательнойy2(в первое уравнениеx2входит с положительным коэффициентом, а в третьем — отсутствует).

Поменяем местами переменныеx2 и y2— первую исключим

из числа свободных, а вторую — включим. Для этого разрешим второе уравнение (2.6) относительноx2и подставимx2в первое уравнение. Получим следующий вид системы (2.5):
x3=x1-y2-x4+5

y2=-3x1-2y2+y1-2x4+8 (2.7)

y3=3x1-5x4+7
Выразим Z через новые свободные переменные:

Z=3x1+2y2-y1+2x4-8+y1-2=3x1+2y2+2x4-10 (2.8)

Полагаяx1=y1=y2=x4=0, получим Z = -10.

Это решение является оптимальным, так как коэффициенты при всех свободных переменных в выражении (2.8) неотрицательны. Итак, оптимальное решение ОЗ найдено (2.9):

x1*=0, x2*=8, x3*=5, x4*=0, y1*=0, y2*=0, y3*=7. (2.9)

При таких значениях переменных линейная функция Z принимает минимальное значение (2.10):
Zmin=-10 (2.10)
Заметим, что в рассмотренном примере нам не пришлось искать опорное решение: оно сразу же получилось, когда мы положили свободные переменные равными нулю. Это объясняется тем, что в уравнениях (2.5) все свободные члены были неотрицательны и, значит, первое же попавшееся решение оказалось опорным. Если это окажется не так, можно будет прийти к опорному решению с помощью такой же процедуры обмена местами некоторых базисных и свободных переменных, повторно решая уравнения до тех пор, пока свободные члены не станут неотрицательными