Цель работы. Изучение графических возможностей электронных таблиц MS Excel, приобретение навыков работы с Мастером диаграмм в электронных таблицах.
Задание. Построить графики функций из табл. 2 – 5.
Таблица 2. Варианты заданий
| № | f(x) | № | f(x) | № | f(x) |
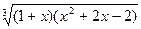 | 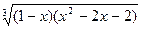 | 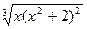 | |||
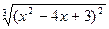 | 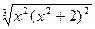 | 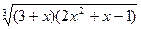 | |||
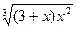 | 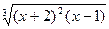 | 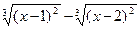 | |||
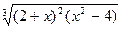 | 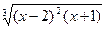 | 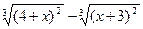 | |||
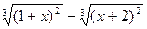 | 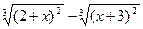 | 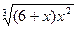 | |||
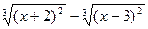 | 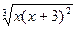 | 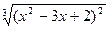 | |||
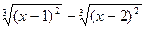 | 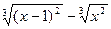 | 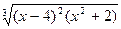 | |||
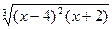 | 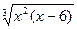 | 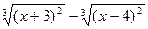 | |||
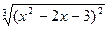 | 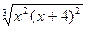 | 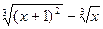 | |||
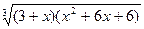 | 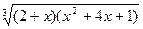 | 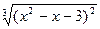 |
Таблица 3. Варианты заданий
| № | f(x) | № | f(x) | № | f(x) |
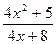 | 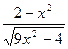 | 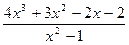 | |||
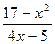 | 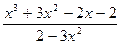 | 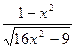 | |||
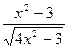 | 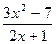 | 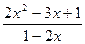 | |||
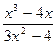 | 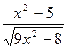 | 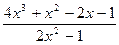 | |||
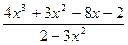 | 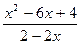 | 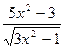 | |||
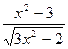 | 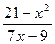 | 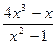 | |||
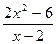 | 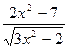 | 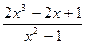 | |||
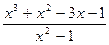 | 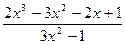 | 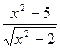 | |||
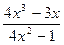 | 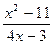 | 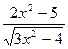 | |||
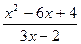 | 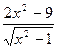 | 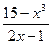 |
Таблица4. Варианты заданий
| № | f(x) | № | f(x) | № | f(x) |
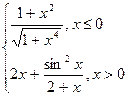 | 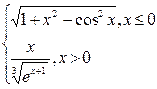 | 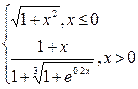 | |||
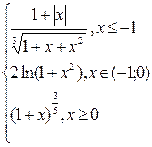 | 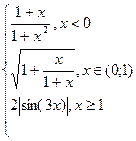 | 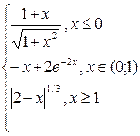 | |||
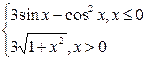 | 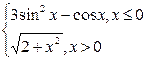 | 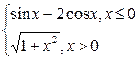 | |||
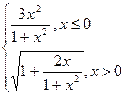 | 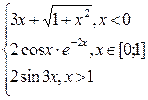 | 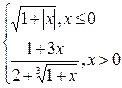 | |||
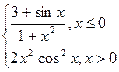 | 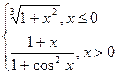 | 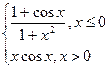 | |||
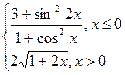 | 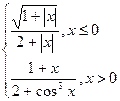 | 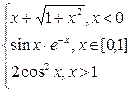 | |||
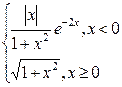 | 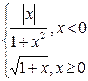 | 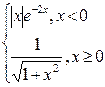 | |||
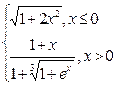 | 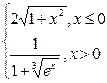 | 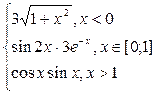 | |||
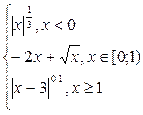 | 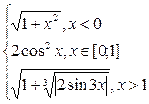 | 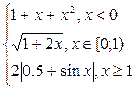 | |||
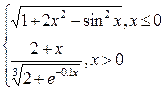 | 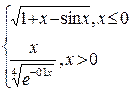 | 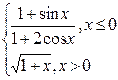 |
Таблица5. Варианты заданий
| № | f(x,y) | № | f(x,y) | № | f(x,y) |
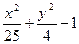 | 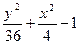 | 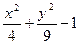 | |||
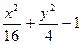 | 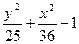 | 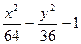 | |||
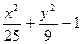 | 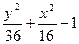 | 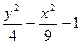 | |||
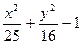 | 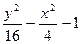 | 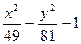 | |||
| y2 - 2x2 - 4 | y2 +4x2 - 4 | 2y2 - 9x2 –18 | |||
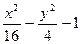 | 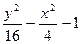 | 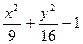 | |||
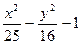 | 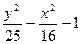 | 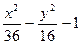 | |||
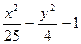 | 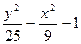 | 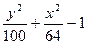 | |||
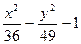 | 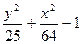 | 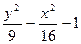 | |||
| 9y2 - 4x2 – 16 | 9y2 + 4x2 – 16 | 2y2 +9x2 – 81 |
Рекомендации к выполнению лабораторной работы. Рассмотрим несколько примеров.
ПРИМЕР 1. Построить график функции 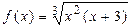 .
.
1. Определим функцию f(x).
В ячейки А1:А21 введем значение аргумента при помощи автозаполнения (например, с шагом 0,5). В ячейку В1 введем значение функции, вычисляемое по формуле В1 =(A1^2*(A1+3))^(1/3). Ячейки В2:В21 заполняются копированием формулы из ячейки В1.
2. Выделим диапазон А1:В21 и воспользуемся Мастером диаграмм. Для построения графика функции лучше выбрать точечную диаграмму, со значениями, соединенными сглаживающими линиями без маркеров.
| Чтобы график получился выразительным, можно определить промежуток изменения аргумента, увеличить толщину линий, выделить оси координат, нанести на них соответствующие деления, сделать подписи на осях и вывести заголовок. | 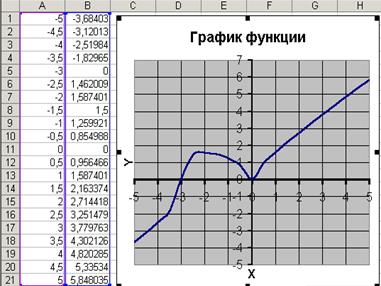 Рис. 7. Рис. 7. |
ПРИМЕР 2. Построить график функции 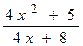 .
.
При построении этого графика следует обратить внимание на область определения функции. В данном случае функция не существует при обращении знаменателя в ноль.
Решим уравнение: 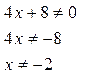 Следовательно, при определении значений аргумента следует помнить, что при Следовательно, при определении значений аргумента следует помнить, что при 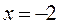 функция не определена. Зададим значение аргумента в два этапа, не включая (-2) с шагом 0.2. функция не определена. Зададим значение аргумента в два этапа, не включая (-2) с шагом 0.2. | 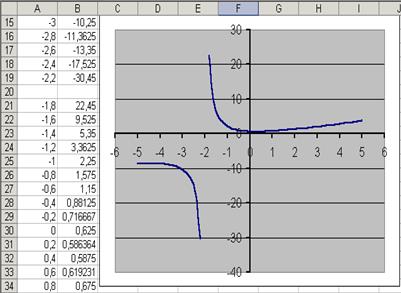 Рис. 8 Рис. 8 |
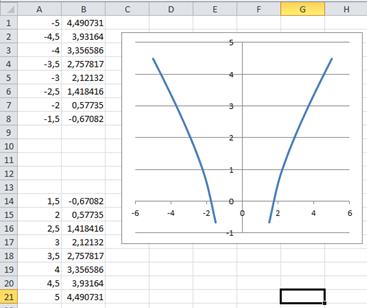 Рис. 9. Рис. 9. | ПРИМЕР 3. Построить график функции 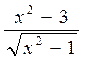 . ОДЗ: . ОДЗ: 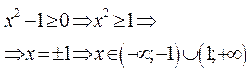 Определение значения аргумента следует провести в два этапа. Например, от -5 до -1, а затем от 1 до 5. Определение значения аргумента следует провести в два этапа. Например, от -5 до -1, а затем от 1 до 5. |
ПРИМЕР 5. Изобразите линию заданную неявно уравнением:
4 y 2 +5 x 2 – 20=0.
Заданная уравнением f(x,y)=0 функция описывает кривую линию под названием эллипс. Это можно доказать, если произвести элементарные математические операции:
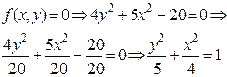
Разрешим заданное уравнение относительно переменной y:
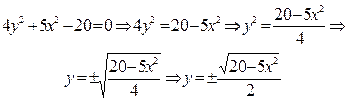
Линию f(x,y) можно изобразить, построив графики двух функций:
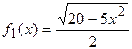 и
и 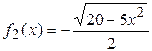
в одной графической области.
Определим ОДЗ функций 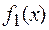 и
и 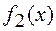 .
.
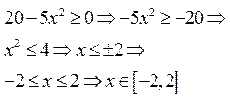
Для построения графика введем значения аргумента в диапазон А3:А43 (от -2 до 2, D=0,1).
В ячейку В3 введем формулу для вычисления значений функции 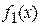 :
:
В3=КОРЕНЬ(20-5*$A3^2)/2.
А в ячейку С3 для вычисления значений функции 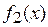 :
:
С3=-КОРЕНЬ(20-5*$A3^2)/2.
Далее скопируем эти формулы до В43 и С43 соответственно.
Затем выделим диапазон А3:С43 и воспользовавшись Мастером диаграмм, построим графики функций 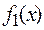 и
и 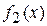 в одной графической области.
в одной графической области.
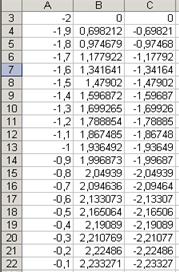
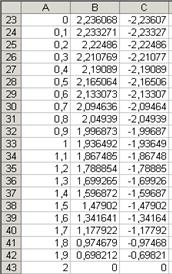
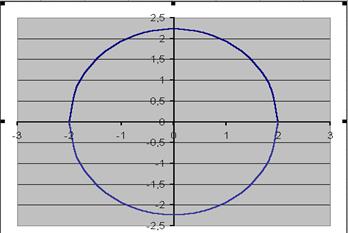
Рис. 10.
ПРИМЕР 6. Изобразите линию заданную неявно: 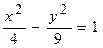 .
.
Данное уравнение описывает линию под названием гипербола. Разрешим его относительно переменной y:
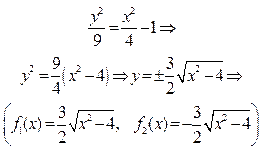 Найдем ОДЗ Найдем ОДЗ 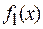 и и 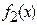 : : 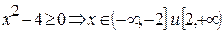 | 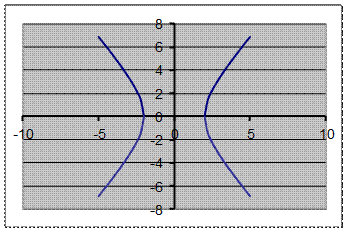 Рис. 11 Рис. 11 |
ПРИМЕР 7. Построить график функции 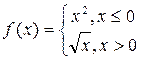
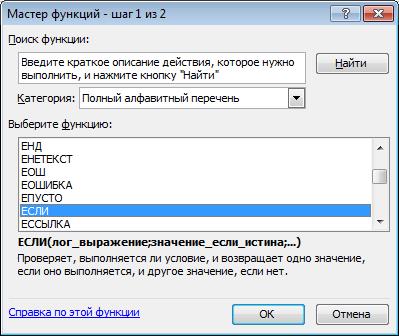
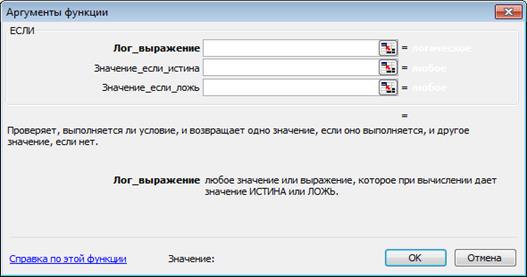
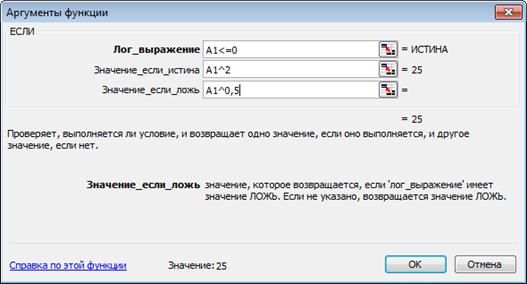
Рис. 12
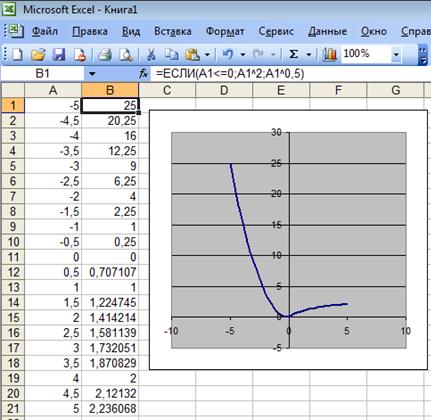
Рис. 13
ПРИМЕР 8. Построить график функции
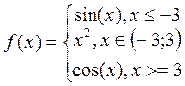
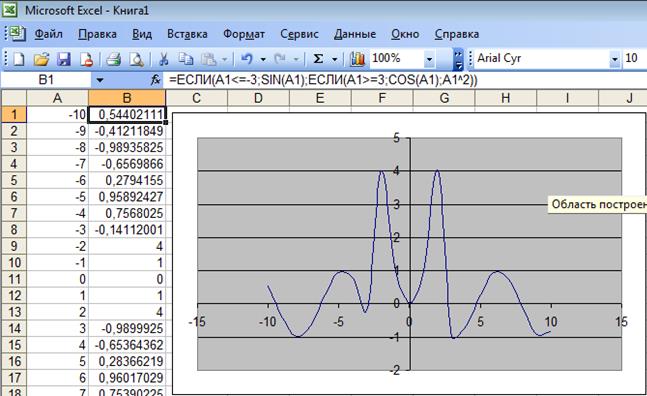
Рис. 14
ЛАБОРАТОРНАЯ РАБОТА №4
 2015-05-13
2015-05-13 3424
3424
