Основные элементарные функции

Обратная функция. Пусть есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому единственное значение, при котором. Тогда полученная функция, определенная на множестве Y с областью значений Х, называется обратной.

Так как традиционно независимую переменную обозначают через х, а функцию – через у, то функция, обратная к функции , примет вид 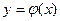. Обратную функцию  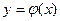обозначают также в виде  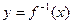(аналогично с обозначением обратной величины). Например, для функции y  a^x обратной будет функция x log _ay, или (в обычных обозначениях зависимой и независимой переменных) .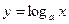

Можно доказать, что для любой строго монотонной функции 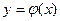 существует обратная функция.

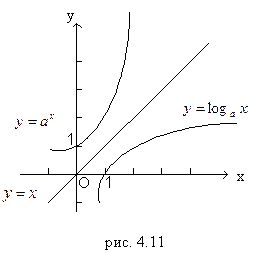
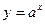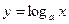Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций и  при ).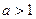

Сложная функция. Пусть функция 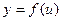 есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией  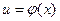от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция  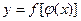называется сложной функцией (функцией от функции). Например,  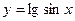- сложная функция, так как ее можно представить в ви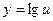де , где .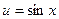

Элементарные функции. Классификация функций. Преобразования графиков.

Функция называется явной, если она задана формулой , в которой правая часть не содержит зависимой переменной. Например, .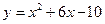

Функция у называется неявной, если она задана уравнением 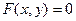, неразрешенным относительно зависимой переменной. Например, 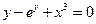. Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например,  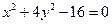- функция задана неявно. Приведем к явному виду: .

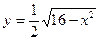Графиком уравнения 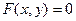 называется множество точек плоскости хОу, координаты которых удовлетворяют этому уравнению.

К основным элементарным функциям относятся:

1. Степенные функции , , , 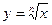где n – натуральное ().

2. Показательные функции (, ).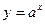

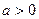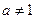3. Логарифмические функции (, ).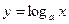

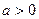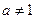4. Тригонометрические функции , , , .

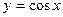5. Обратные тригонометрические функции , , , .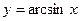

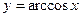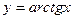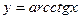Понятие элементарной функции.

Из основных функций новые функции могут быть получены двумя способами:

а) с помощью алгебраических действий;

б) с помощью операций образования сложной функции.

Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Например, функция

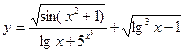
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции (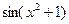, , 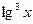, , 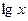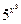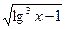) конечно.

Краткий обзор свойств основных элементарных функции представлен в таблице.

Таблица
Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность	Графики функций
1. Степенная функция
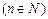	(-∞;+∞)	(-∞;+∞), если n – нечетно [0;+∞), если n - четно	Нечетная, если n – нечетно; четная, если n – четно	Возрастает на (-∞;+∞), если n – нечетно; убывает на (-∞;0], если n – четно	Неперио-дическая
Продолжение таблицы
	(-∞;0)U U(0;+∞)	(-∞;0)U U(0;+∞)если n – нечетно [0;+∞), если n – четно	Нечетная, если n – нечетно; четная, если n – четно	Убывает на (-∞;0) и на (0;+∞), если n – нечетно; возрастает на (-∞;0) и убывает на (0;+∞), если n – четно	Неперио-дическая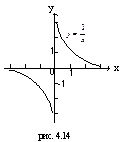
	(-∞;+∞) если n – нечетно [0;+∞) если n – четно	(-∞;+∞), если n – нечетно [0;+∞), если n - четно	Нечетная, если n – нечетно; общего вида, если n – четно	Возрастает на (-∞;+∞), если n – нечетно; возрастает на [0;+∞), если n – четно	Неперио-дическая
2. Показательная функция
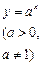	(-∞;+∞)	(0;+∞)	общего вида	Возраст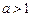ает на (-∞;+∞), если ; убывает на (-∞;+∞), если	Неперио-дическая
3. Логарифмическая функция
	(0;+∞)	(-∞;+∞)	общего вида	Возраст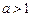ает на (0;+∞), если ; убывает на (0;+∞), если	Неперио-дическая
Продолжение таблицы
4. Тригонометрические функции
	(-∞;+∞)	[-1;1]	нечетная	Возрастает на [-π/2+2π n; π/2+2π n ]; убывает на [π/2+2π n; 3π/2+2π n ],	Период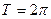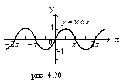
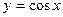	(-∞;+∞)	[-1;1]	четная	Возрастает на [-π+2π n; 2π n ]; убывает на [2π n; π+2π n ],	Период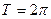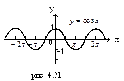
	(-π/2+ +π n; π/2+π n);	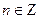(-∞;+∞)	нечетная	Возрастает на (-π/2+π n; π/2+π n);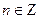	Период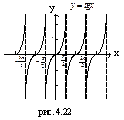
	(π n; π+π n);	(-∞;+∞)	нечетная	Убывает на (π n; π+π n);	Период
5. Обратные тригонометрические функции
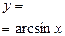	[-1;1]	[-π/2; π/2]	нечетная	Возрастает на [-1;1]	Неперио-дическая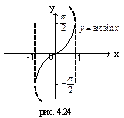
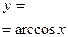	[-1;1]	[0;π]	общего вида	Убывает на [-1;1]	Неперио-дическая
Продолжение таблицы
	(-∞;+∞)	(-π/2; π/2)	нечетная	Возрастает на (-∞;+∞)	Неперио-дическая
	(-∞;+∞)	(0;π)	общего вида	Убывает на (-∞;+∞)	Неперио-дическая

Классификация функций.

Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.

К числу алгебраических функций относятся:

- целая рациональная функция (многочлен или полином):

;

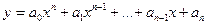- дробно-рациональная функция – отношение двух многочленов;

- иррациональная функция (если в составе операций над аргументом имеется извлечение корня).

Всякая не алгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся: показательная, логарифмическая, тригонометрические, обратные тригонометрические, гиперболические функции.