2015-05-13
6593
1. Построить верхнюю (четные варианты) или нижнюю (нечетные варианты) часть эллипсоида, заданного уравнением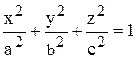 
. Варианты заданий представлены в табл. 6.
2. Построить однополостный (четные варианты) или двухполостный (нечетные варианты) гиперболоид, заданный уравнением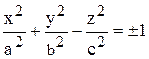 
. Знак плюс относится к уравнению однополостного гиперболоида, знак минус – к уравнению двухполостного гиперболоида. Варианты заданий представлены в табл. 7.
3. Построить эллиптический (четные варианты) или гиперболический (нечетные варианты) параболоид, заданного уравнением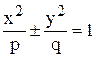 
. Знак плюс относится к уравнению эллиптического параболоида, знак минус – к уравнению гиперболического параболоида. Варианты заданий представлены в табл.8.
Таблица 6. Варианты заданий
| № | a | b | с | № | a | b | c |
| 3.1 | 3.2 | 5.3 | |||||
| 0.9 | 1.1 | 1.25 | 1.95 | 1.5 | |||
| 1.5 | 1.25 | 1.95 | |||||
| 0.71 | 0.75 | 1.21 | |||||
| 1.72 | 2.9 | 3.1 | |||||
| 5.71 | 4.75 | 4.21 | 7.1 | 7.5 | 4.21 | ||
| 2.72 | 3.9 | 5.1 | 7.2 | 8.9 | |||
| 1.5 | 0.78 | 1.45 | 1.5 | 2.78 | 3.45 |
Таблица 7. Варианты заданий
| № | a | b | с | № | a | b | c |
| 3.1 | 3.2 | 5.3 | |||||
| 0.9 | 1.1 | 1.25 | 1.95 | 1.5 | |||
| 1.5 | 1.25 | 1.95 | |||||
| 0.71 | 0.75 | 1.21 | |||||
| 1.72 | 2.9 | 3.1 | |||||
| 5.71 | 4.75 | 4.21 | 7.1 | 7.5 | 4.21 | ||
| 2.72 | 3.9 | 5.1 | 7.2 | 8.9 | |||
| 1.5 | 0.78 | 1.45 | 1.5 | 2.78 | 3.45 |
Таблица 8. Варианты заданий
| № | p | q | № | p | q |
| 1.5 | 2.5 | ||||
| 2.5 | 1/5 | ||||
| 1.4 | 3.4 | ||||
| 3.4 | 1.4 | ||||
| 2.5 | 5.6 | ||||
| 5.4 | 2/5 | ||||
| 1.1 | 4.1 | ||||
| 4.1 | 1.2 | ||||
| 1.5 | 5.1 | ||||
| 5.5 | 1.5 | ||||
| 3.3 | 5.3 | ||||
| 5.1 | 3.7 | ||||
| 4.1 | 5.1 | ||||
| 5.3 | 4.2 | ||||
| 6.05 | 1.9 |
Рекомендации к выполнению лабораторной работы.
ПРИМЕР 1. Построить поверхность z=x2-y2 при x, y Î[-1;1].
В диапазон B1:L1 введем последовательность значений переменной x: -1, -0.8, …,1, а в диапазон ячеек А2:А12 последовательность значений переменой y. В ячейку В2 введем формулу =$A2^2-B$1^2. Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой – абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:L12 в них будет найдено значение z для соответствующих значениях x, y. Таким образом, будет создана таблица значений z.
Для построения поверхности выделим диапазон ячеек A1:L12, содержащий таблицу значений функции. Далее обратимся к Мастеру диаграмм ивыберемтип диаграммы Поверхность. Затем заполним диалоговые окна в соответствии с вариантом задания и получим трехмерный график, показанный на рис 15.
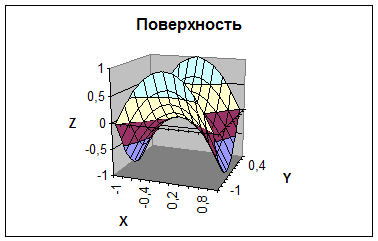
Рис.15. Поверхность вида z=x2-y2
ПРИМЕР 2. Построить верхнюю часть эллипсоида, заданного уравнением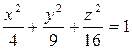 
.
Выразим z через x и y.
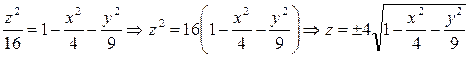
Выражение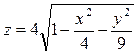 
описывает верхнюю часть эллипсоида.
Найдем область определения функции z (x, y).
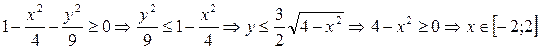
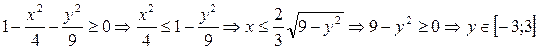
Выполним построения как в предыдущем примере (рис. 16).
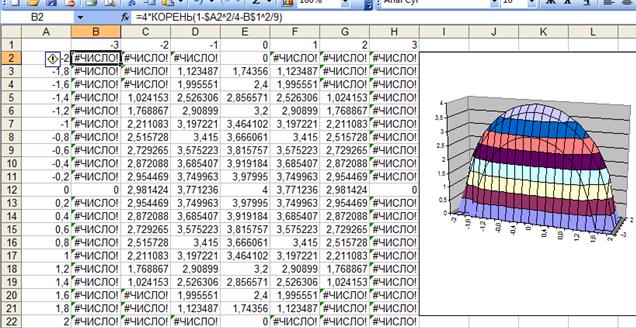
Рис.16
ПРИМЕР 3. Построить двухполосный гиперболоид, заданный уравнением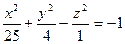 
.
Выразим z через x и y.
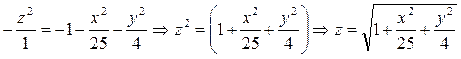
Функция определена везде. Выполним построения (рис. 17).
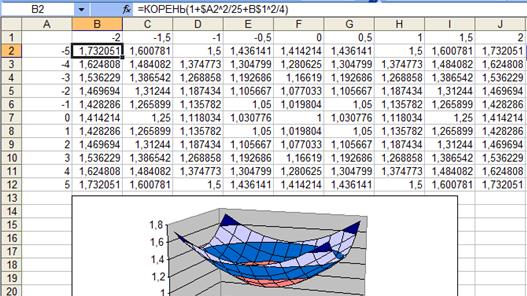
Рис. 17
ПРИМЕР 3. Построить однополосный гиперболоид, заданный уравнением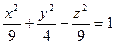 
.
Выразим z через x и y.
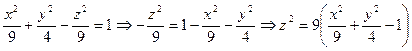
Выражение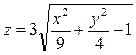 
описывает однополосный гиперболоид.
Найдем область определения функции z (x, y).
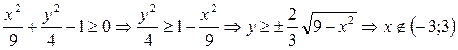
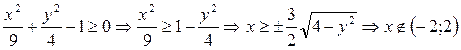
Выполним построения (рис. 18).
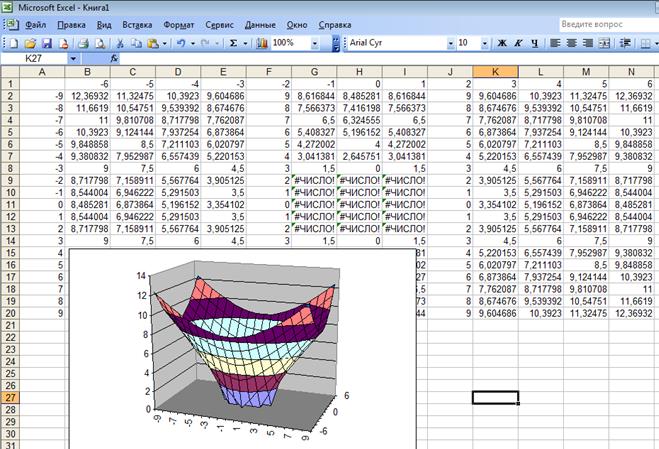
Рис. 18.
Лабораторная работа №5
