1. Найти решение системы линейных алгебраических уравнений с помощью обратной матрицы, выполнить проверку.
2. Найти решение системы линейных уравнений методом Крамера.
3. Выполнить действия над матрицами.
Вариант №1 1) 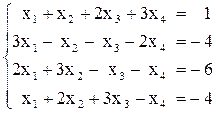 2)
2) 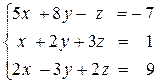
3) 2 (A + B) (2B – A), 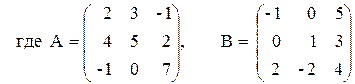
Вариант №2 1) 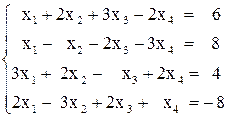 2)
2) 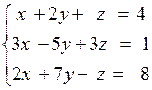
3) 3 A - (A + 2B) B, 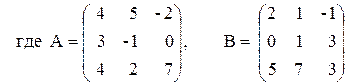
Вариант № 3 1) 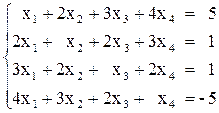 2)
2) 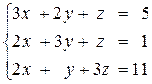
3) 2(A–B)(A2 + B), 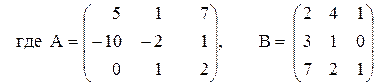
Вариант №4 1) 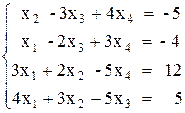 2)
2) 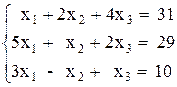
3) (A2 – B2)(A + B), 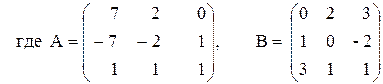
Вариант №5 1) 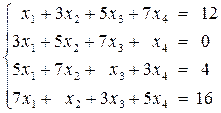 2)
2) 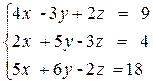
3) (A–B2)(2A+B), 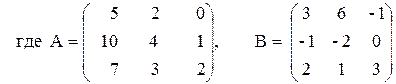
Вариант №6 1) 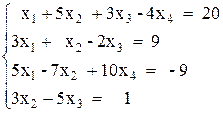 2)
2) 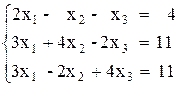
3) (A – B) A + 2B, 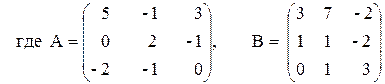
Вариант №7 1) 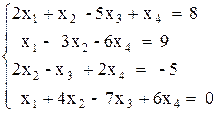 2)
2) 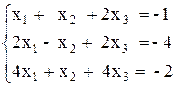
3) 2(A–0,5B)+AB, 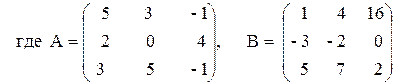
Вариант №8 1) 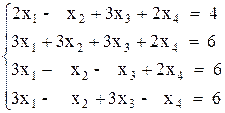 2)
2) 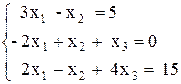
3) (A – B)A + 3B, 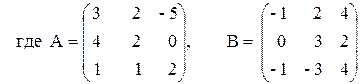
Вариант №9 1) 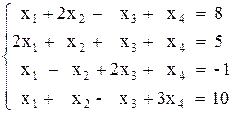 2)
2) 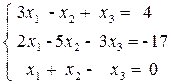
3) 2A – (A2 + B) B, 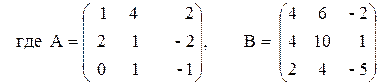
Вариант №10 1) 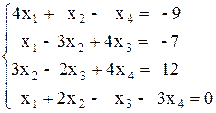 2)
2) 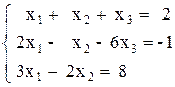
3) 3 (A2 – B2) –2АB, 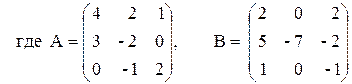
Вариант №11 1) 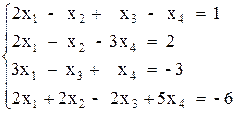 2)
2) 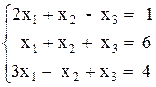
3) (2A–B)(3А+B)–2АВ, 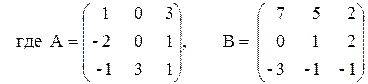
Вариант №12 1) 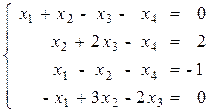 2)
2) 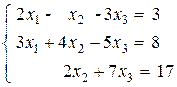
3) А(A2–B)-2(B+А)В, 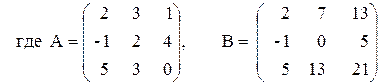
Вариант №13 1) 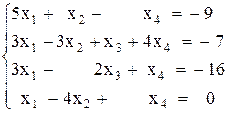 2)
2) 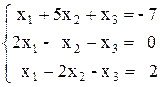
3) (A+B)A–B(2А+3В), 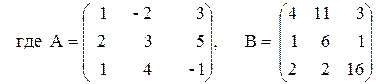
Вариант №14 1) 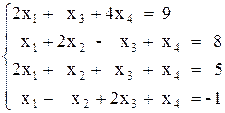 2)
2) 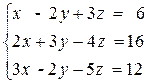
3) A(2A+B)–B(А–В), 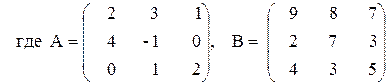
Вариант №15 1) 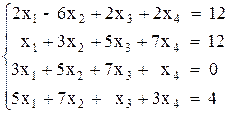 2)
2) 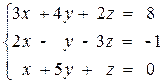
3) 3(A+B)(AВ–2А), 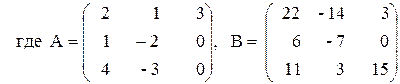
Вариант №16 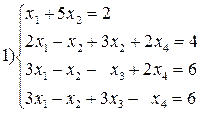 2)
2) 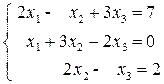
3) 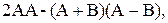 где
где 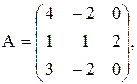
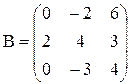
Вариант №17 1) 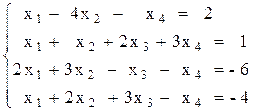 2)
2) 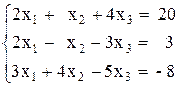
3) 2А + 3B(АB-2А), 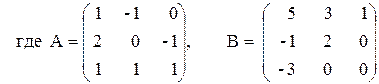
Вариант №18 1) 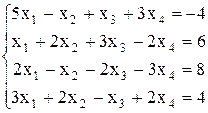 2)
2) 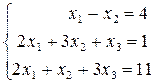
3) 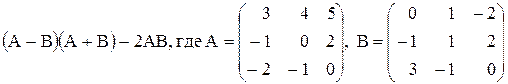
Вариант №19 1) 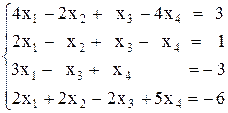 2)
2) 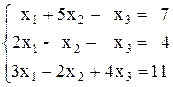
3) 2A - АB(В - А) + В, 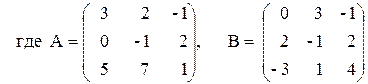
Вариант №20 1) 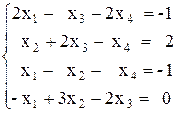 2)
2) 
3) A2 - (A + B)–(А – 3В), 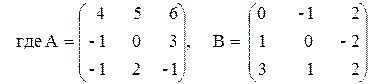
Вариант №21 1) 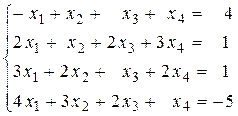 2)
2) 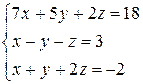
3) 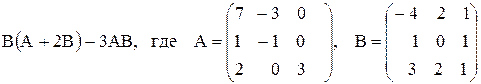
Вариант№22 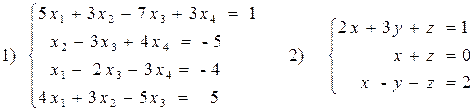
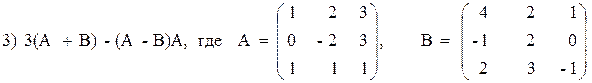
Вариант №23 1) 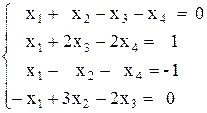 2)
2) 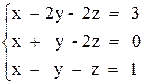
3) А(A - B) + 2В(A + В), 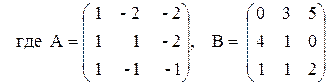
Вариант№24 1) 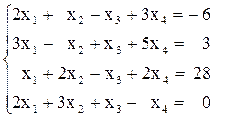 2)
2) 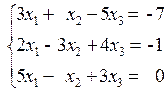
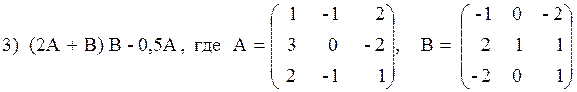
Вариант№25 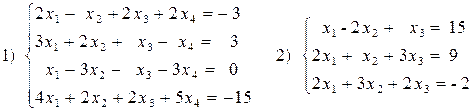
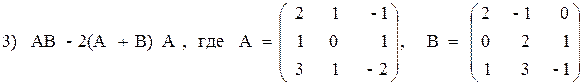
Вариант №26 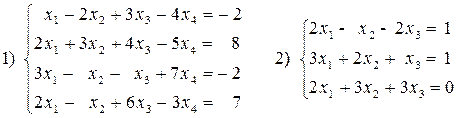
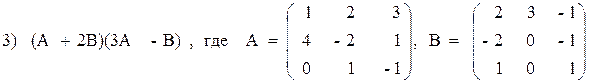
Вариант №27 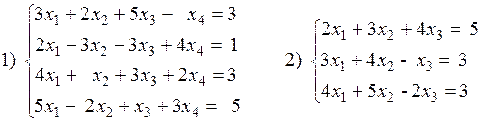
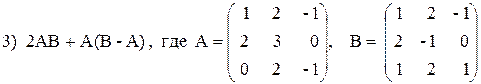
Вариант №28 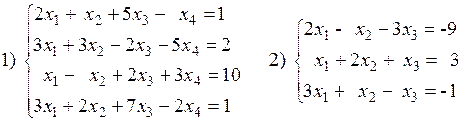
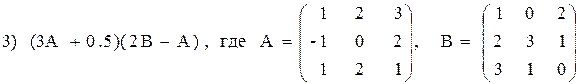
Вариант№29 
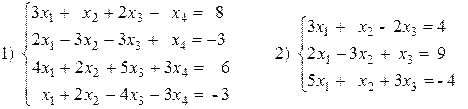
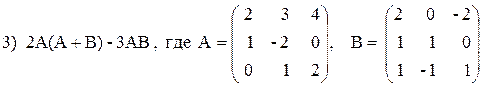
Вариант №30 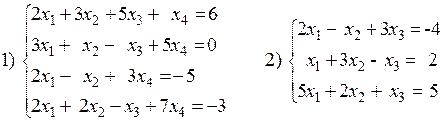
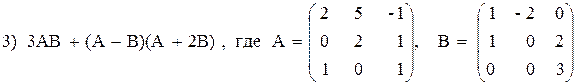
Рекомендации к выполнению лабораторной работы.
Предварительно вспомним некоторые сведения из курса высшей математики, необходимые для выполнения данной лабораторной работы.
Решение систем линейных алгебраических уравнений (СЛАУ).
Пусть задана СЛАУ следующего вида:
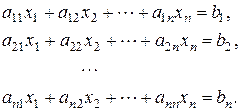
Эту систему можно представить в матричном виде: AX=b, где
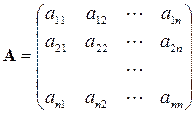 – матрица коэффициентов системы уравнений;
– матрица коэффициентов системы уравнений;
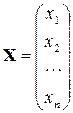 – вектор неизвестных,
– вектор неизвестных, 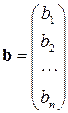 – вектор правых частей.
– вектор правых частей.
При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.
Метод обратной матрицы.
Систему линейных алгебраических уравнений Ax=b умножим слева на матрицу, обратную к А. Система уравнений примет вид:
A-1.A.x=A-1.b, E.x=A-1.b, (E – единичная матрица)
Таким образом, вектор неизвестных вычисляется по формуле x=A-1.b.
Метод Крамера.
В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:
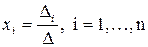
где D – определитель матрицы A, Di – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Рассмотрим несколько примеров. Обратите внимание на особенность работы с матричными функциями в Ms Excel: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Пример 1. Решить систему методом обратной матрицы:
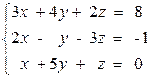
Идея решение СЛАУ методом обратной матрицы заключается в следующем. Заданную систему записывают в матричной форме Ax=b, где A – матрица коэффициентов СЛАУ при неизвестных, b – вектор правых частей, x – вектор неизвестных, который вычисляют по формуле x=A-1.b, причем A-1. – это матрица обратная к A. Реализовать эту идею в MS Excel можно следующим образом. Введём матрицу A и вектор b в рабочий лист MS Excel (Рис. 4). Пусть матрица А находится в ячейках B1:D3, а вектор b в диапазоне F1:F3. Выделим ячейки для хранения обратной матрицы, пусть это будут ячейки B5:D7.
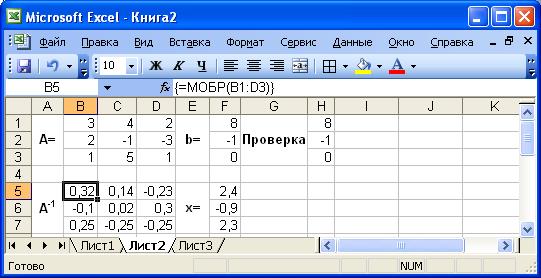
Рис. 4. Решение СЛАУ методом обратной матрицы
Обратимся к Мастеру функций, и в категории Математические выберем функцию МОБР, предназначенную для вычисления обратной матрицы. В качестве аргумента этой функции укажем диапазон ячеек, в котором хранится матрица A, т.е. МОБР(B1:D3) [34]. Теперь умножим полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например F5:F7. Обратимся к Мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. У этой функции два аргумента – диапазоны перемножаемых матриц. Введем в качестве первого аргумента диапазон ячеек, в котором содержится обратная матрица, а в качестве второго – ячейки, содержащие вектор b, т.е. МУМНОЖ (B5:D7;F1:F3). Вектор неизвестных хранится в ячейках F5:F7. Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x иполучить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(B1:D3; F5:F7).
Пример 2. Решить систему из примера 2 методом Крамера.
В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:
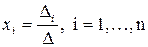
где D – определитель матрицы A, Di – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Введём матрицу А и вектор b в рабочий лист. Сформируем три вспомогательные матрицы, заменяя последовательно столбцы матрицы A на вектор b ( Рис. 5). Вычислим определитель матрицы A. Установим курсор в ячейку B5 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную длявычисления определителя матрицы. В качестве аргумента зададим диапазон ячеек, в котором хранится матрица A:
 2015-05-13
2015-05-13 956
956








