Для функции одной переменной локальные экстремумы следует искать только среди ее критических точек (т.е. точек, в которых производная функции равна 0 или не существует) и на границах допустимого множества.
ПРИМЕР 2. Решить ЗМП 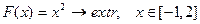 .
.
► Существование решения этой задачи обеспечено TW. Найдем критические точки целевой функции, принадлежащие допустимому множеству. Производная целевой функции 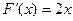 определена всюду и обращается в нуль при
определена всюду и обращается в нуль при 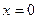 . Поскольку при
. Поскольку при 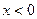 производная отрицательна, а при
производная отрицательна, а при 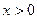 – положительна, найденная критическая точка является локальным минимумом. Задача имеет решение либо в точке
– положительна, найденная критическая точка является локальным минимумом. Задача имеет решение либо в точке 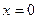 (внутренний локальный экстремум), либо на концах промежутка: в точке
(внутренний локальный экстремум), либо на концах промежутка: в точке 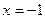 , либо в точке
, либо в точке 
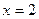 (граничные локальные экстремумы). Найдем значения целевой функции в этих точках:
(граничные локальные экстремумы). Найдем значения целевой функции в этих точках: 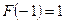 ,
, 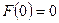 ,
, 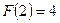 .
.
Выберем среди них наибольшее и наименьшее. Таким образом, получаем:
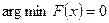 ,
, 
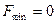 ,
, 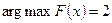 ,
, 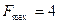 ◄
◄
 2015-05-13
2015-05-13 861
861








