Числовые и функциональные ряды

Числовым рядом называется формальное выражение вида

,

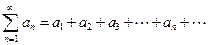где число слагаемых 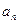неограниченно. Выражение 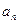называется общим, или 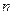-ным, членом ряда. Сумме бесконечного числа слагаемых нужно придать смысл. Делается это следующим образом. Назовем 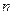–ной частичной суммой ряда 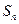сумму первых 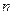слагаемых

.

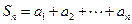Суммой ряда 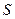называется предел частичных сумм

.

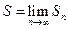Ряд с конечной суммой называется сходящимся. Если предела частичных сумм не существует, говорят, что ряд расходится.

Найти сумму ряда точно почти никогда не удается. В действительности важно знать, сходится ли ряд вообще, или нет. Именно этот вопрос нас и будет интересовать.

Необходимое условие сходимости ряда

.

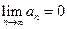Ряд называется знакоопределенным, если все слагаемые имеют один знак. Имеется несколько простых достаточных условий сходимости знакоположительных рядов.

Признак Даламбера. Пусть существует предел

.

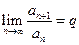Тогда, если 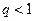, то ряд 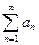сходится; если 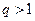, то ряд расходится.

Признак Коши (радикальный). Пусть существует предел

.

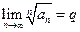Если 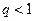, то ряд 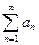сходится, если 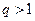, то ряд 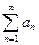расходится.

Признак Коши (интегральный). Если найдется такая монотонно убывающая положительная функция 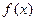, что 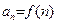для всех 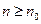, то тогда из сходимости интеграла 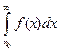следует сходимость ряда 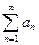, а из расходимости интеграла 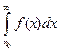следует расходимость ряда .

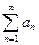Иногда для исследования сходимости знакоположительного ряда удобно использовать признаки сравнения. Если 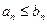и ряд 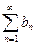сходится, то и 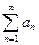сходится. Если 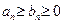и ряд 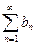расходится, то и 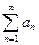расходится.

Из признаков сходимости знаконеопределенных рядов нам потребуется признак Лейбница сходимости знакочередующегося ряда. Если мы имеем ряд

,

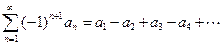где 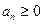, 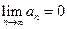и при этом 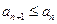, то ряд 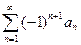сходится. Для рядов, удовлетворяющих условию Лейбница (то есть знакочередущихся рядов, у которых монотонный предел модуля 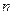–го члена равен нулю), имеется следующая полезная оценка:

,

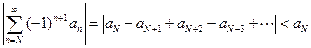то есть остаток ряда, начиная с произвольного члена 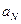, по модулю не превосходит этого члена.

Задача 4.5.а Исследовать сходимость ряда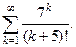

Решение. Имеем 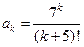, , 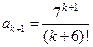и, по признаку Даламбера,

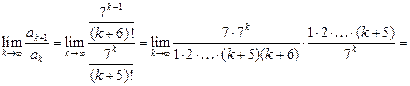
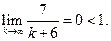Следовательно, ряд сходится.

Задача 4.5.б Исследовать сходимость ряда .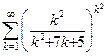

Решение. Имеем: 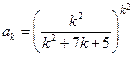, и, по радикальному признаку Коши,

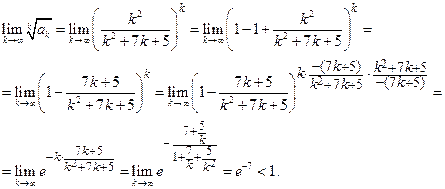Следовательно, ряд сходится.

Литература.

1. Щипачев В.С. Высшая математика. Учебник для вузов. - М., Высшая школа, 2001.

2. Кремер Н.Ш. Высшая математика для экономистов. Учебник. 2 издание. Юнити - Дана, 2002.

3. Г.Я Волошин- Курс высшей математики для экономистов. Учебное пособие. М.2003.

4. П.Е. Данко, А.Г. Попов, Т.Я. Кожевников – Высшая математика в упражнениях и задачах.

Част 1. М. «В.Ш.» 1999г.