Производной функции 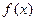 в точке
в точке 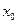 называется предел
называется предел
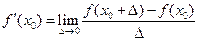 .
.
Наряду с обозначением 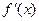 для производной используется еще обозначение
для производной используется еще обозначение 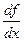 .
.
Производные основных элементарных функций приведены в следующей таблице.
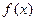
| 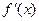
|
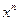
| 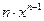
|
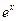
| 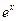
|
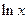
| 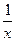
|
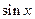
| 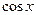
|
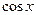
| 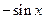
|
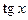
| 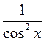
|
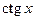
| 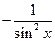
|
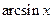
| 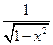
|
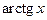
| 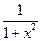
|
Имеется два основных приема дифференцирования функций
1) Формуладифференцирования произведения и частного двух функций
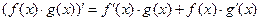 ,
,
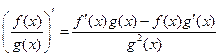 .
.
2) Формула дифференцирования композиции (или сложной функции)
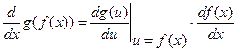 .
.
В задачах 2.2.а-2.2.з для функции 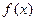 требуется найти производную
требуется найти производную 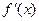 .
.
Задача 2.2.а 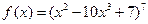 .
.
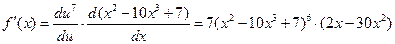 .
.
Задача 2.2.б 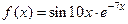 .
.
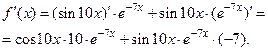
Задача 2.2.в 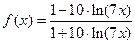 .
.
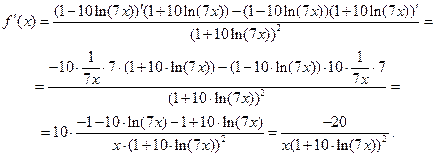 Задача 2.2.г
Задача 2.2.г 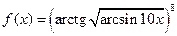 .
.
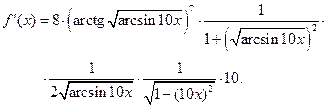
Задача 2.2.д 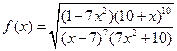 .
.
Решение. При дифференцировании этой функции удобно воспользоваться приемом, который называется логарифмическим дифференцированием. Прежде чем вычислять производную, найдем логарифм функции 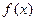 :
:
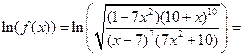
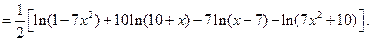
Теперь продифференцируем правую и левую часть полученной формулы, а затем приравняем соответствующие производные. Имеем:
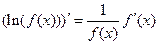 ;
;
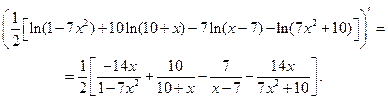
Отсюда,
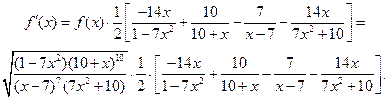
Задача 2.2.е 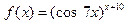 .
.
Решение. Здесь также удобно воспользоваться приемом логарифмического дифференцирования.
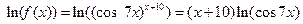 ;
;
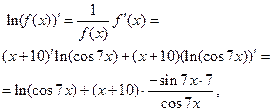
откуда следует, что
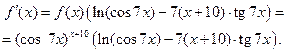
Задача 2.2.ж 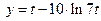 ,
, 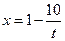 .
.
Решение. Функция 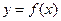 задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
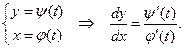
Получаем:
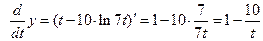 ,
,
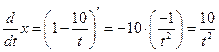 ,
,
откуда
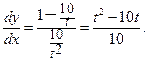
Задача 2.2.з 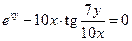 .
.
Решение. Функция 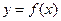 задана неявным уравнением. Чтобы найти производную
задана неявным уравнением. Чтобы найти производную 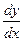 , продифференцируем тождество
, продифференцируем тождество 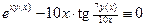 . Получаем:
. Получаем:
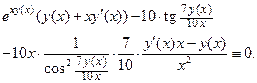
Перегруппируем слагаемые, выделяя члены, содержащие производную 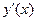 :
:
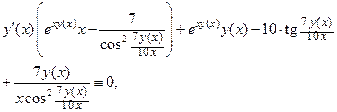
откуда следует, что
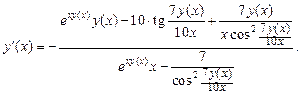
 2015-05-13
2015-05-13 358
358








