Уравнений

Если определитель матрицы 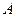системы линейных уравнений равен нулю (или число уравнений системы меньше числа неизвестных), то либо имеется бесконечно много решений, либо система противоречива, и решений нет вовсе. Разберем на примере, как можно описать все решения вырожденной системы уравнений, используя метод Гаусса последовательного исключения неизвестных.

Задача 1.2. Решить систему уравнений

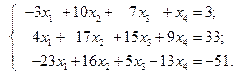
Решение. С помощью первого уравнения исключим переменную 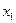из второго и третьего уравнений системы.

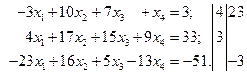
Получаем:

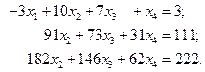
Исключим теперь с помощью второго уравнения системы переменную 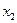из третьего уравнения.

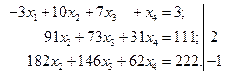
В результате третье уравнение системы превращается в тождество 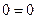, и остается только два уравнения:

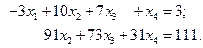
Мы привели систему к верхнетреугольному виду, однако для двух неизвестных (а именно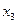, для и для 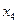) не хватило “своего” уравнения для преобразования исключения. В этом случае переменные 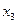, 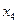объявляются свободными (то есть их значения могут выбираться произвольным образом), а значения остальных переменных (они называются базисными) могут быть выражены через значения свободных переменных.

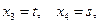
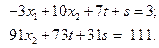
Отсюда:

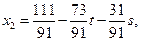
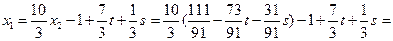
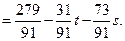
Ответ: 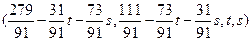, где 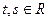- произвольные параметры.