Задача 2.4. Исследовать функцию 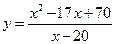 с помощью производных первого и второго порядка и построить её график.
с помощью производных первого и второго порядка и построить её график.
Решение. Исследование функции производится по следующей схеме.
1. Общие особенности функции: область определения, непрерывность и точки разрыва, вертикальные асимптоты, четность – нечетность, периодичность.
В нашем случае область определения функции
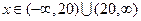 ;
;
прямая 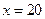 – вертикальная асимптота, функция общего вида.
– вертикальная асимптота, функция общего вида.
2. Нули функции и интервалы знакопостоянства.
Применим метод интервалов для исследования знаков функции.
 - + - +
- + - +
7 10 20 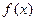
3. Возрастание – убывание функции, точки экстремума. Этот пункт связан с исследованием знаков первой производной функции. Имеем:
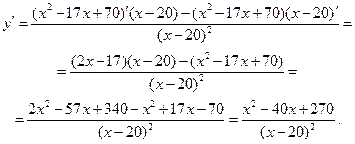
Корни квадратного многочлена 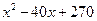 равны
равны
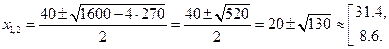
Знаки 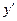 определим, используя метод интервалов.
определим, используя метод интервалов.
 + - - +
+ - - + 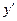
8.6 20 31.4
 max
max 
 min
min 
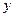
Точки 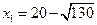 и
и 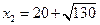 являются точками локального максимума и минимума соответственно.
являются точками локального максимума и минимума соответственно.
4. Выпуклость – вогнутость функции, точки перегиба. Данный пункт связан с исследованием второй производной функции. Если 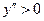 , то функция выпукла вверх (как функция
, то функция выпукла вверх (как функция 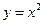 ), а если
), а если 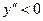 , то функция выпукла вниз (как функция
, то функция выпукла вниз (как функция 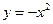 ).
).
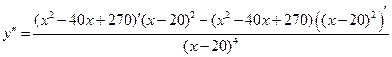
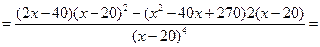
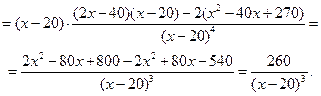

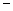 +
+ 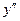
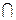 20
20 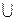
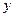
5. Наклонные асимптоты функции.
Наклонная асимптота функции (если она существует) есть такая прямая 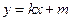 на плоскости
на плоскости 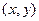 , к которой “прижимается” график функции
, к которой “прижимается” график функции 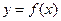 при
при 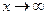 , то есть
, то есть 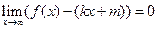 . Коэффициенты
. Коэффициенты 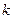 и
и 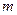 определяются из соотношений
определяются из соотношений
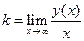 ,
, 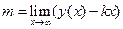 .
.
В нашем случае
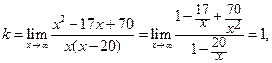
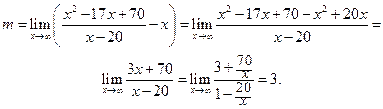
Следовательно, прямая 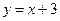 является наклонной асимптотой функции.
является наклонной асимптотой функции.

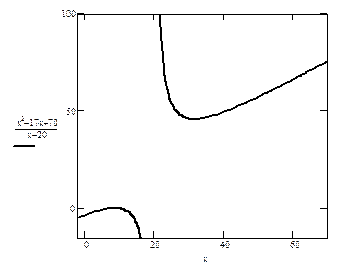
 |
 2015-05-13
2015-05-13 307
307








