Продолжим рассмотрение примера, приведенного в разделе 2.4. Воспользовавшись тем, что взаимодействие факторов 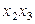 и
и 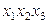 оказалось статистически незначимым, исследуем влияние на качество поверхности магнитных дисков скорости нагрева
оказалось статистически незначимым, исследуем влияние на качество поверхности магнитных дисков скорости нагрева 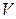 и изотермической выдержки
и изотермической выдержки 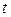 , поставив для этой цели ДФЭ типа
, поставив для этой цели ДФЭ типа 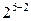 . Условия проведения опытов сведем в табл. 3.4.
. Условия проведения опытов сведем в табл. 3.4.
Таблица 3.4
Условия проведения ДФЭ
| Характеристика плана | 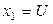 , B , B | 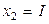 , A , A | 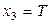 , , 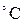 | 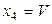 , , 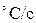 | 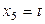 , , 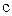 |
| Нулевой уровень | |||||
| Интервал варьирования | |||||
| Верхний уровень | |||||
| Нижний уровень |
В этом случае ДФЭ позволяет построить полиномиальную ММ следующего вида:
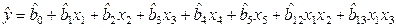 .
.
Для факторов 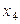 и
и 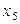 генераторами плана выберем взаимодействия
генераторами плана выберем взаимодействия 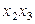 и
и 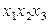 , тогда контрасты будут соответственно
, тогда контрасты будут соответственно
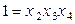 и
и 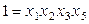 ,
,
а обобщающий контраст
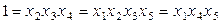 .
.
Найдем смешанность оценок:
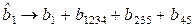 ;
;
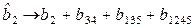 ;
;
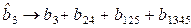 ;
;
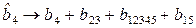 ;
;
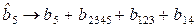 ;
;
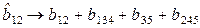 ;
;
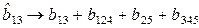 .
.
Cоставим МП эксперимента, в соответствии с которой проведем рандомизированные опыты. Полученные результаты запишем в табл. 3.5, где 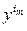 – численные значения исследуемого параметра,
– численные значения исследуемого параметра, 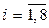 – номер точки в факторном пространстве,
– номер точки в факторном пространстве, 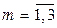 – номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
– номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
Проведем статистическую обработку полученных результатов. Для проверки по критерию Кохрена (2.3) воспроизводимости опытов при выбранном уровне значимости 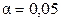 вычислим в каждой точке факторного пространства среднее значение
вычислим в каждой точке факторного пространства среднее значение
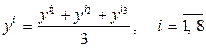
и оценку дисперсии
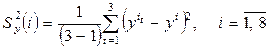 .
.
Критическое значение 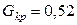 найдем из таблицы G-распределения (прил. 4) при
найдем из таблицы G-распределения (прил. 4) при 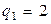 ,
, 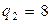 . С помощью соотношения (2.3) найдем
. С помощью соотношения (2.3) найдем 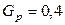 . Поскольку
. Поскольку 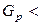
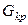 , считаем, что дисперсии наблюдений во всех точках факторного пространства однородны.
, считаем, что дисперсии наблюдений во всех точках факторного пространства однородны.
Рассчитаем оценки коэффициентов регрессионного уравнения 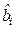 . Для этого составим матрицу
. Для этого составим матрицу 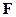 :
:
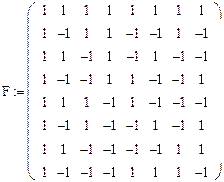
и найдем дисперсионную матрицу 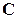
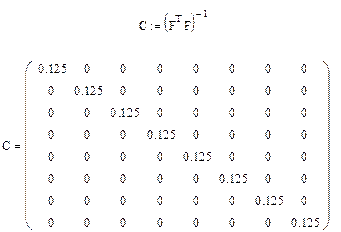
Вычислим оценки 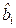 коэффициентов
коэффициентов 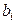
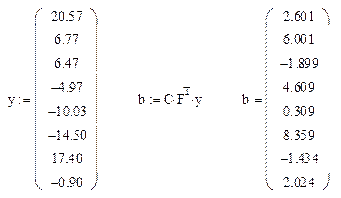
По критерию Стьюдента с использованием соотношения (2.4) определим статистическую значимость коэффициентов регрессии при 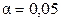 , для которого при
, для которого при 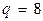 критическое значение
критическое значение 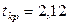 . При этом оценки дисперсий всех оценок
. При этом оценки дисперсий всех оценок 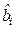 одинаковы
одинаковы
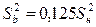 ,
,
где 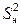 – оценка дисперсии единичного наблюдения, вычисленная по соотношению (2.5).
– оценка дисперсии единичного наблюдения, вычисленная по соотношению (2.5).
В нашем случае она равна 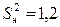 , следовательно,
, следовательно, 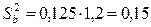 . Поэтому
. Поэтому 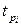 вычисляются как
вычисляются как 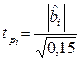 . Исключим из ММ незначимый коэффициент регрессии
. Исключим из ММ незначимый коэффициент регрессии 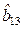 . При этом благодаря ортогональности плана оценки остальных коэффициентов не изменятся.
. При этом благодаря ортогональности плана оценки остальных коэффициентов не изменятся.
По критерию Фишера проверим адекватность линейной ММ при 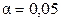 . Для этого нужны оценки дисперсий единичного наблюдения и неадекватности. Дисперсия единичного наблюдения уже найдена и равна
. Для этого нужны оценки дисперсий единичного наблюдения и неадекватности. Дисперсия единичного наблюдения уже найдена и равна 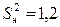 . Вычислим дисперсию неадекватности
. Вычислим дисперсию неадекватности
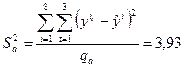 ,
,
где 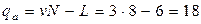 .
.
Находим 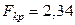 по таблице F-распределения (прил. 6) при
по таблице F-распределения (прил. 6) при 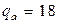 и
и 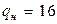 . Так как
. Так как 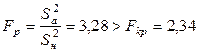 , то линейная модель неадекватна. Необходимо добавить эффект взаимодействия с наибольшим по модулю коэффициентом –
, то линейная модель неадекватна. Необходимо добавить эффект взаимодействия с наибольшим по модулю коэффициентом – 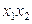 . Теперь
. Теперь 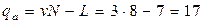 ,
, 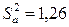 . При этом
. При этом 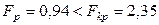 , то есть модель адекватна. Делаем вывод о том, что полученная ММ с уровнем значимости
, то есть модель адекватна. Делаем вывод о том, что полученная ММ с уровнем значимости 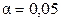 не противоречит экспериментальным результатам.
не противоречит экспериментальным результатам.
Переходим к натуральному масштабу:
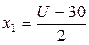 ,
, 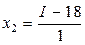 ,
, 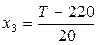 ,
, 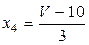 ,
, 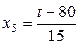 ,
,
где 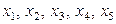 ‑ нормированные значения,
‑ нормированные значения, 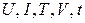 – значения в натуральном масштабе.
– значения в натуральном масштабе.
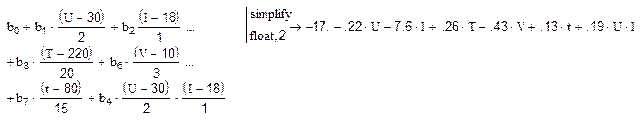
Получаем ММ:
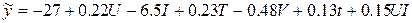 ,
,
где 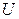 – опорное напряжение, В;
– опорное напряжение, В; 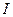 – ток потребления, А;
– ток потребления, А; 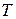 – конечная температура нагрева,
– конечная температура нагрева, 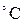 ;
; 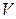 – скорость нагрева,
– скорость нагрева, 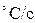 ;
; 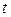 – изотермическая выдержка, c.
– изотермическая выдержка, c.
 2015-05-13
2015-05-13 1028
1028








