2015-05-13
948
При наличии в ММ взаимодействий, оценки коэффициентов при линейных членах остаются независимыми друг от друга, однако они могут быть смешаны с оценками высших порядков, а часть оценок коэффициентов при парных взаимодействиях оказывается смешанной друг с другом. Например, если рассмотреть модель, содержащую все возможные коэффициенты для ДФЭ типа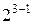 
с генератором 
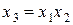, то получим МП, представленную в табл. 3.3. Из таблицы видно, что порядок чередования знаков 
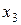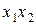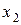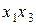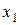и 
, 
и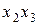 
, 
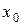и 
, 
и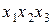 
одинаков. Это означает, что в таком эксперименте невозможно получить раздельные, независимые оценки для коэффициентов 
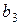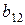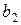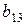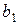и 
(
и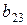 
, 
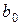и 
, 
и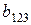 
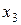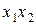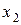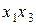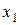), а можно получить лишь оценку, характеризующую суммарное воздействие фактора и взаимодействия ( и 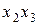, 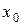и , и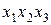 
).
Таблица 3.3
МП ДФЭ типа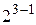 
, содержащая взаимодействия
| 
| 
| 
| 
| 
| 
| 
| 
|
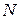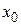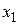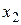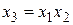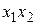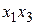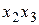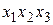| +1 +1 +1 +1 | –1 +1 –1 +1 | –1 –1 +1 +1 | +1 –1 –1 +1 | +1 –1 –1 +1 | –1 –1 +1 +1 | –1 +1 –1 +1 | +1 +1 +1 +1 |
При значительном числе факторов и опытов определение смешанности по МП является трудоемким. Для нахождения, при каких факторах и взаимодействиях оценки коэффициентов будут смешанными, вводят понятие «контраст плана». Контраст получают умножением обеих частей генератора плана вводимого дополнительного фактора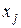 
на этот фактор. Например, поскольку для ДФЭ (табл. 3.1) генератор плана 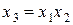, то для контраста получим 
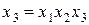, т. к. 
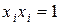, окончательно имеем 
.
|
|
|
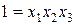Чтобы определить, с какими факторами и взаимодействиями смешана оценка фактора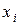 
, необходимо умножить обе части контраста на этот фактор. Например, для 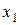имеем: 
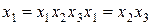, т. е. 
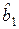оценивает одновременно коэффициенты 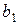и 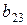. Это можно записать так
.
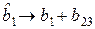Для :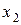 
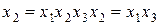, тогда 
;
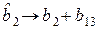для :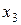 
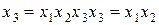, тогда 
.
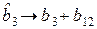Сравнивая с табл. 3.1, можно убедиться в соответствии результатов.
В зависимости от числа факторов, входящих в контраст, говорят о разрешающей способности ДФЭ. Так, если для ДФЭ типа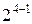 
в качестве генератора плана выбрано 
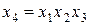(контраст соответственно будет 
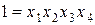), то говорят, что у такого эксперимента разрешающая способность равна четырем; если генератор 
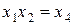и контраст 
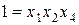, то разрешающая способность равна трем. Дробные факторные эксперименты с наибольшей разрешающей способностью называют главными и отдают им предпочтение.
Если вводится не один, а несколько дополнительных факторов, то получаем несколько генераторов плана (для каждого дополнительного фактора свой). В этом случае для определения смешанности оценок используют обобщающий контраст, который строится из отдельных контрастов, а также их произведений во всевозможных сочетаниях. Пусть, например, для ДФЭ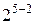 
в качестве генераторов выбраны соотношения 
, 
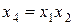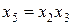и 
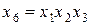, контрасты будут соответственно , 
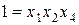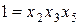и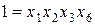 
, а обобщающий контраст:
|
|
|
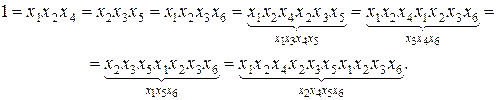
Для определения смешанности оценок перемножают все составляющие обобщающего контраста на соответствующие факторы:
– для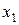 
: 
;
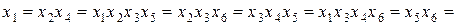
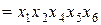– для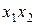 
: 
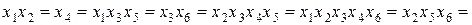
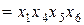и т. д.
Тогда для смешанности оценок получим:
;
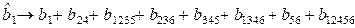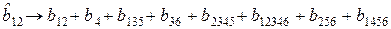и т. д.
Необходимо отметить, что следствием уменьшения числа опытов по сравнению с ПФЭ является и уменьшение точности оценок, вызванное их смешанностью.
