Число степеней свободы

Понятие числа степеней свободы непосредственно связано с несмещенностью оценок некоторой суммы квадратов. Пусть имеется 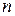случайных переменных 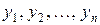и существует 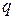линейных связей между ними. Тогда говорят, что сумма квадратов 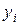имеет 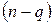степеней свободы. То же самое можно сформулировать и следующим образом. Пусть среди случайных переменных 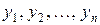имеется ровно 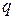попарно независимых, а 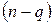линейно связаны, то есть существует 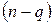линейных зависимостей, связывающих 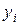. Тогда говорят, что сумма квадратов 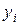имеет 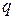степеней свободы.

Так, например, в ПФЭ и ДФЭ при исследовании адекватности ММ используют оценку дисперсии единичного наблюдения

.

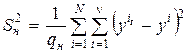Здесь 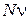слагаемых, связанных 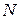линейными связями ( 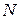вычислений для средних значений 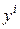), соответственно .

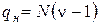ПРИЛОЖЕНИЕ 3