Проверка статистических гипотез. Под гипотезойв данных методических указаниях понимается некоторое предположение о случайной величине

Под гипотезой в данных методических указаниях понимается некоторое предположение о случайной величине. Примерами могут служить гипотезы об однородности дисперсий во всех точках факторного пространства, о значимости коэффициентов регрессии, об адекватности математической модели.

Необходимость выдвижения гипотез возникает при обработке или интерпретации результатов наблюдений. Проверка статистических гипотез – один из разделов математической статистики. При проверке гипотезы необходимо установить, насколько экспериментальные результаты согласуются с выдвинутой гипотезой, после чего принять или отвергнуть гипотезу.

Правило, в соответствии с которым принимается или отвергается данная гипотеза, называется статистическим критерием. Построение критерия сводится к выбору подходящей функции 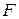от результатов наблюдений, служащей мерой расхождения между экспериментальным и гипотетическим законами.

При решении вопроса о принятии или отклонении гипотезы с помощью какого-либо статистического критерия, основанного на результатах эксперимента, могут быть допущены ошибки двух типов. Ошибка «первого рода» совершается тогда, когда гипотеза отвергается, а на самом деле она верна, «второго рода» - когда гипотеза принимается, а на самом деле она не верна.

Результаты проверки гипотезы никогда не могут служить доказательством абсолютной справедливости и правильности гипотезы. Они означают лишь то, что гипотеза с заданной вероятностью не противоречит результатам эксперимента. Поэтому при проверке гипотезы нужно заранее допустить возможность ошибочного решения. Вероятность того, что гипотеза будет отвергнута при условии, что она верна, называют уровнем значимости и обозначают 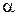. Тогда величина 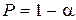, называемая статистической надежностью, характеризует вероятность выполнения статистического критерия при условии, что гипотеза верна. В технических задачах, как правило, выбирают 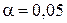или 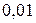, что соответствует уровню значимост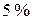и и .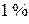

По распределению функции 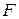находят критическое значение 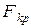такое, что если гипотеза верна, то вероятность неравенств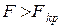а равна 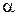. Если рассчитанное по результатам эксперимента значение 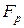функции 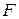больше 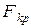, считают, что расхождение значимо и гипотеза отвергается. Если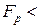 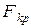, то экспериментальные данные не противоречат гипотезе.